Direkte Verfahren zur Lösung von linearen Gleichungssystemen
Die direkten Verfahren zur Lösung des linearen Gleichungssystems
mit quadratischer Koeffizientenmatrix (n Gleichungen mit n Unbekannten) liefern die Lösung nach einer endlichen Anzahl von Rechenschritten (im Gegensatz zu den iterativen Verfahren, bei denen man sich der Lösung sukzessive annähert, siehe auch: "Direkte Verfahren vs. Iterationsverfahren"). Die mit Abstand am häufigsten verwendeten direkten Verfahren sind der Gaußsche Algorithmus und das Verfahren von Cholesky.
Einschränkungen der Anwendbarkeit der Verfahren
- Für die Anwendung des Gaußschen Algorithmus ist die Eigenschaft "Matrix A ist regulär" die einzige notwendige Voraussetzung. Für die Anwendung des Cholesky-Verfahrens müssen noch zwei weitere Eigenschaften dieser Matrix zwingend vorausgesetzt werden.
-
Das Cholesky-Verfahren funktioniert nur bei symmetrischer Koeffizientenmatrix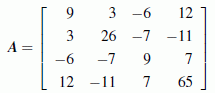
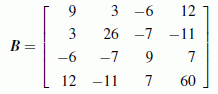
Zwei symmetrische Matrizen, die sich kaum unterscheiden (nur im Element unten rechts: 65 bzw. 60), nur eine ist positiv definit. Man kann diese Eigenschaft nicht erkennen (das Cholesky-Verfahren überprüft sie).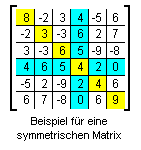 
Die Elemente einer symmetrischen Matrix sind zur Hauptdiagonalen (im Beispiel gelb unterlegt) spiegelbildlich gleich.
Das bedeutet auch, dass die Elemente einer Zeile gleich sind mit den Elementen der entsprechenden Spalte (hier für die 4. Zeile bzw. Spalte farblich gekennzeichnet). A. Dies ist eine Einschränkung für die Anwendbarkeit, die auch dann noch nicht für die Nutzung des Cholesky-Verfahrens spricht, wenn diese Bedingung erfüllt ist. Die Vorteile einer symmetrischen Matrix (der Aufwand für die Lösung halbiert sich) können auch vom Gaußschen Algorithmus genutzt werden. - Das Cholesky-Verfahren setzt voraus, dass die Koeffizientenmatrix A positiv definit ist. Dies ist eine recht starke Einschränkung.
Warum überhaupt "Cholesky"?
Nachdem oben beschrieben wurde, dass das Verfahren von Cholesky stark einschränkende Bedingungen voraussetzt, bleibt die Frage, warum nicht generell der Gaußsche Algorithmus verwendet werden sollte.
Die Beschränkung der Anwendbarkeit des Cholesky-Verfahrens auf positiv definite Matrizen ist die eigentliche Stärke dieses Verfahrens. Die mathematischen Modelle im naturwissenschaftlich-technischen Bereich (und insbesondere in der Technischen Mechanik), die auf lineare Gleichungssysteme führen (speziell Diskretisierungsverfahren wie die Methode der finiten Elemente oder das Differenzenverfahren) erzeugen fast ausschließlich positiv definite Matrizen.
Wenn man weiß, dass ein Verfahren auf ein Gleichungssystem mit symmetrischer, positiv definiter Koeffizientenmatrix führt, sollte man unbedingt das Cholesky-Verfahren benutzen, weil es automatisch diese Eigenschaft überprüft.
Wenn die Lösung eines linearen Gleichungssystems falsch ist, ist fast immer der Mensch die Ursache: Er kann sich (bei der Handrechnung) verrechnen, oder er kann (bei der Computernutzung) falsche Werte eingeben. Besonders häufig ist aber eine richtige Lösung für ein fehlerhaft formuliertes Gleichungssystem. Während der Gaußsche Algorithmus fast immer (Ausnahme ist nur die singuläre Koeffizientenmatrix) ein Ergebnis abliefert, dem man in der Regel nicht ansieht, ob es richtig oder falsch ist, darf man bei Benutzung des Cholesky-Verfahrens hoffen (mehr leider nicht), dass das Verfahren ein falsches (oder fehlerhaft eingegebenes) Gleichungssystem erkennt.
Ist es überhaupt wahrscheinlich, dass eine Matrix nicht positiv definit ist?
Wenn eine Koeffizientenmatrix, die theoretisch positiv definit sein müsste, einen oder mehrere Fehler enthält, braucht sie natürlich nicht gleich die Eigenschaft der positiven Definitheit zu verlieren. Es ist aber erstaunlich, wie häufig schon bei kleinen Fehlern in der Matrix das Cholesky-Verfahren genau aus diesem Grunde versagt.
Man kann sich mit einem kleinen Test eine sehr gute Vorstellung davon verschaffen, wie schwierig es ist, überhaupt eine positiv definite Matrix zu erzeugen. Unter TM-interaktiv findet man das Programm "Cholesky" mit dem Angebot, für eine einzugebende Matrix die Cholesky-Zerlegung durchzuführen. Nach dem Programmstart ist das Eingabeschema für eine Matrix mit 3 Zeilen bzw. Spalten vorbereitet, dies kann jedoch beliebig geändert werden. Nachfolgend sieht man, wie der Versuch in den meisten Fällen endet:
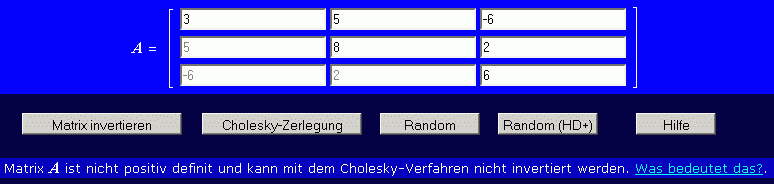
Nach Eingabe der 6 Werte, die diese kleine Matrix definieren, wurde der Button "Cholesky-Zerlegung" angeklickt, und es erscheint die Mitteilung, dass dies nicht möglich ist. Nach mehreren Versuchen mit jeweils geänderter Matrix kann man durchaus Glück haben, mal eine positiv definite Matrix zu erzeugen. Man kann auch den Button "Random" benutzen, um Zufallsmatrizen zu erzeugen (alle Elemente liegen im Bereich −100 ≤ ai j ≤ 100), immer abwechselnd auf diesen Button und den Button "Cholesky-Zerlegung" klicken, um ein Gefühl zu bekommen, wie relativ selten zufällig eine positiv definite Matrix entsteht. Bei Matrizen mit 3 Zeilen bzw. Spalten hat man noch gelegentlich Glück, wem es gelingt, eine positiv definite Zufallsmatrix mit 6 Zeilen bzw. Spalten zu erzeugen, der sollte unbedingt Lotto spielen.
Ganz fair ist der Button "Random" allerdings nicht, weil er tatsächlich
alle Elemente zufällig erzeugt. Der nachfolgende Bildschirm-Schnappschuss
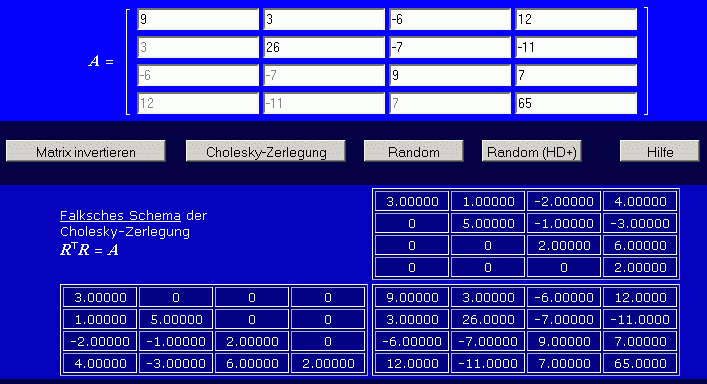
einer erfolgreichen Cholesky-Zerlegung, die in Form der
Rückrechnung
RTR = A
nach dem
Falkschen Schema
Beispiel für Matrixmultiplikation
dargestellt wird, zeigt, dass die Diagonalelemente
ai i aus dem Vektorprodukt der
i-ten Zeile von
RT mit der
i-ten Spalte von
R entstehen, so dass nur
die Quadrate der Elemente dieser Zeile/Spalte addiert werden.
Auf der Hauptdiagonalen von A
entstehen ausschließlich positive Werte (zum Beispiel:
a33 = (−2)·(−2)+(−1)·(−1)+2·2 = 9):
Allgemein gilt:
Der Button "Random (HD+)" berücksichtigt das. Mit ihm werden auch Zufallsmatrizen erzeugt, aber mit der Garantie positiver Hauptdiagonalelemente. Die Chance, damit eine positiv definite Matrix zu erzeugen, ist wesentlich größer, es ist jedoch erstaunlich, wie klein sie immer noch ist. Deshalb gilt:
