Aufgabe
Im Kapitel 35 des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird folgende Aufgabe formuliert:
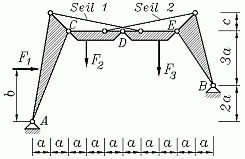
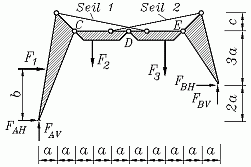
Eine Dachkonstruktion wird für die statische Berechnung wie skizziert modelliert als System aus vier starren Körpern, die untereinander durch Gelenke und zwei einander kreuzende Seile verbunden sind. Es sind die Lager-, Gelenk- und Seilkräfte zu berechnen.
Gegeben: F , F1 = 2F , F2 = F , F3 = 3F , b/a = 3 , c/a = 1 .
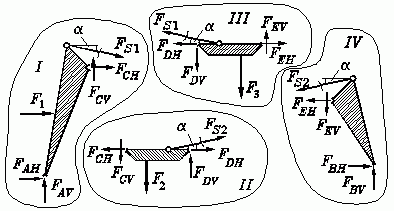
Die nebenstehende Schnittskizze zeigt die freigeschnittenen vier Teilsysteme mit den 12 unbekannten Kräften. Es gilt die Empfehlung: Wenn die Gleichgewichtsbedingungen für die Berechnung mit dem Computer aufbereitet werden, sollten die jeweils einfachsten Bedingungen formuliert werden. Dies sind hier für jedes Teilsystem das Kraft-Gleichgewicht in horizontaler und das Kraft-Gleichgewicht in vertikaler Richtung, außerdem eine Momenten-Gleichgewichtsbedingung, für die jeweils als Bezugspunkt der Seilbefestigungspunkt gewählt wird, so dass die schräg angreifenden Seilkräfte darin nicht erscheinen.
Die 12 Gleichgewichtsbedingungen werden in Matrixform zusammengefasst. Die Abmessung a kürzt sich aus allen Gleichungen heraus, und die Kraft F kann als gemeinsamer Faktor aus dem Vektor der rechten Seite herausgezogen werden, so dass das verbleibende System nur noch gegebene Zahlenwerte enthält:
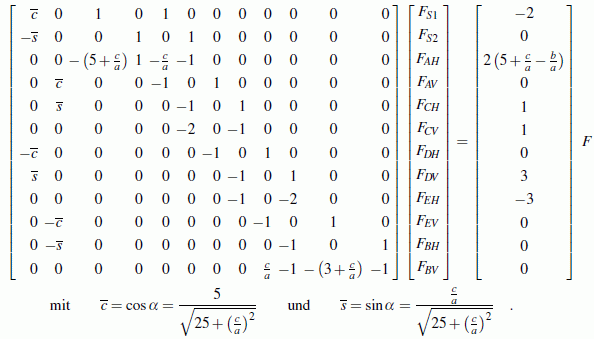
Dieses lineare Gleichungssystem mit 12 Gleichungen und 12 Unbekannten ist eigentlich ein Fall für das Programm "Lineares Gleichungssystem, Matrixinversion". Aber auch das Programm "Überbestimmtes lineares Gleichungssystem" verkraftet diesen Sonderfall und gestattet darüber hinaus das Formulieren zusätzlicher Gleichungen zur Kontrolle, was hier demonstriert werden soll.
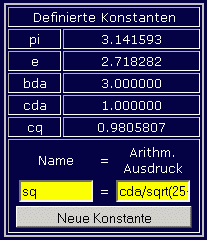
Nach dem Start des Programms werden zunächst die gegebenen Werte b/a (als bda) und c/a (als cda) als Konstanten definiert, und unter Verwendung dieser Werte zusätzlich die Konstanten c (als cq für "c-quer") und s (als sq), die als arithmetische Ausdrücke eingegeben werden können. Rechts sieht man das Konstanten-Fenster mit den vordefinierten Konstanten pi und e, den bereits definierten Konstanten bda, cda und cq und der für die Eingabe vorbereiteten Konstanten sq. Nach Anklicken von "Konstante definieren" ist die Konstanten-Definition abgeschlossen.
Nun wird als Eingabeschema "Matrixform" gewählt, für die Anzahl der Gleichungen m und die Anzahl der Unbekannten n wird jeweils 12 eingetragen, und nach Anklicken von "OK" erweitert sich das Eingabeschema entsprechend. Nach Eintragen aller Werte (auch die Namen der Unbekannten wurden dem aktuellen Problem angepasst) sieht es so aus:


Nun kann "Gleichungssystem lösen" angeklickt werden, und das nebenstehend zu sehende Ergebnis erscheint.
Natürlich können sich auf dem langen Weg bis zu diesem Ergebnis beliebig viele Fehler einschleichen. Kontrollen sind deshalb zwingend, zum Beispiel über drei zusätzliche Bedingungen am Gesamtsystem (nur freigeschnitten von den beiden Lagern:)
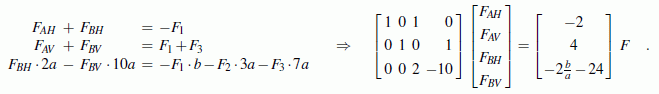
Diese 3 Gleichungen werden dem System der 12 Gleichungen hinzugefügt. Dafür wird zunächst die Anzahl der zu ergänzenden Gleichungen in das Eingabefeld vor dem Button "Gleichungen hinzufügen" eingetragen:

Nach Anklicken des Buttons "Gleichungen hinzufügen" erweitert sich das Eingabeschema. Nachfolgend sind in das erweiterte Schema die zusätzlichen Gleichungen bereits eingegeben:


Nun kann wieder "Gleichungssystem lösen" angeklickt werden, und das nebenstehend zu sehende Ergebnis für das System mit 15 Gleichungen stimmt exakt mit dem oben für 12 Gleichungen gewonnenen Ergebnis über ein.
Das ist ein sehr starkes Indiz für die Richtigkeit der Rechnung. Zusätzliche Bestätigung findet man, indem man einzelne Gleichungen wieder aus dem System herausnimmt (durch Entfernen des "Häkchens" vor den Gleichungen). Der nachfolgende Ausriss zeigt, wie die Gleichungen 4, 5 und 6 entfernt werden. Die Rechnung mit den verbleibenden 12 Gleichungen liefert wieder das korrekte Ergebnis.
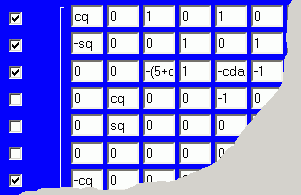
Auswirkungen von Fehlern

Der Mehraufwand mit zusätzlichen Gleichungen lohnt sich natürlich nur dann, wenn er mit der Absicht betrieben wird, Fehler zu entdecken. Der nebenstehend zu sehende Ausriss zeigt für das oben beschriebene Gleichungssystem einen Vorzeichenfehler in der ersten Gleichung.
Ein solcher Fehler kann weder bei der Berechnung mit 12 noch bei der Berechnung mit 15 Gleichungen entdeckt werden. In beiden Fällen werden die "richtigen Ergebnisse für die fehlerhaften Systeme" abgeliefert. Aber die Ergebnisse unterscheiden sich, und genau das ist ein sicheres Indiz für einen Fehler:

|

|
|
| Rechnung mit 12 Gleichungen | Rechnung mit 15 Gleichungen | |
| Die Ergebnisse der beiden Rechnungen sind deutlich voneinander verschieden, wenn sich ein Fehler eingeschlichen hat | ||

