Torsionsproblem: FEM-Lösung der Poissonschen Differenzialgleichung
Weil auf der Seite "Testrechnungen für iterative Verfahren (1)" ein kleines Beispiel beschrieben wird, bei dem die iterativen Verfahren (vorsichtig ausgedrückt) nicht sehr gut aussehen, soll hier als erstes Beispiel ein Gleichungssystem aufgebaut und gelöst werden, bei dem diese Verfahren sich als leistungsstark erweisen.
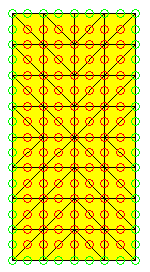
Zur Berechnung des Torsionsträgheitsmoments für einen Rechteckquerschnitt (entnommen aus dem Kapitel "Methode der finiten Elemente") wird ein 6-Knoten-Dreieckselement aus Matlab-Femset verwendet (nebenstehend links ein FEM-Netz mit 64 Elementen). Das Matlab-Script, das dort verwendet wird , muss leicht modifiziert werden, damit das entstehende Gleichungssystem untersucht werden kann.
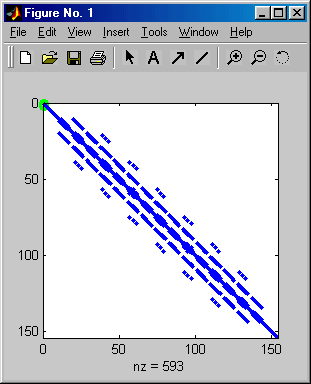
Nachfolgend ist das Matlab-Script zu sehen, mit dem die Rechnungen ausgeführt werden. Wie schon auf der Seite "Testrechnungen für iterative Verfahren (1)" wird das Gleichungssystem mit einer Koeffizientenmatrix als "Sparse matrix" formuliert (rechts ist das Belegungsmuster der Matrix für das links oben zu sehende FEM-Modell zu sehen). Gelöst wird das Gleichungssystem zunächst zu Referenzzwecken mit dem Matlab-Standard-Solver, außerdem mit dem Script KonjugGrad.m aus dem Buch "A. Meister: Numerik linearer Gleichungssysteme" (über den Link http://www.mathematik.uni-kassel.de/~meister/buch-online zum Download verfügbar) und mit 8 von den 9 in Matlab verfügbaren iterativen Lösungsverfahren (gmres wurde aus den Gründen, die hier genannt werden, nicht berücksichtigt).
Die Feinheit der Finite-Elemente-Diskretisierung (und damit die Größe des Gleichungssystems) wird im Script ItVerfTors.m durch die beiden Werte in Zeile 5 festgelegt:
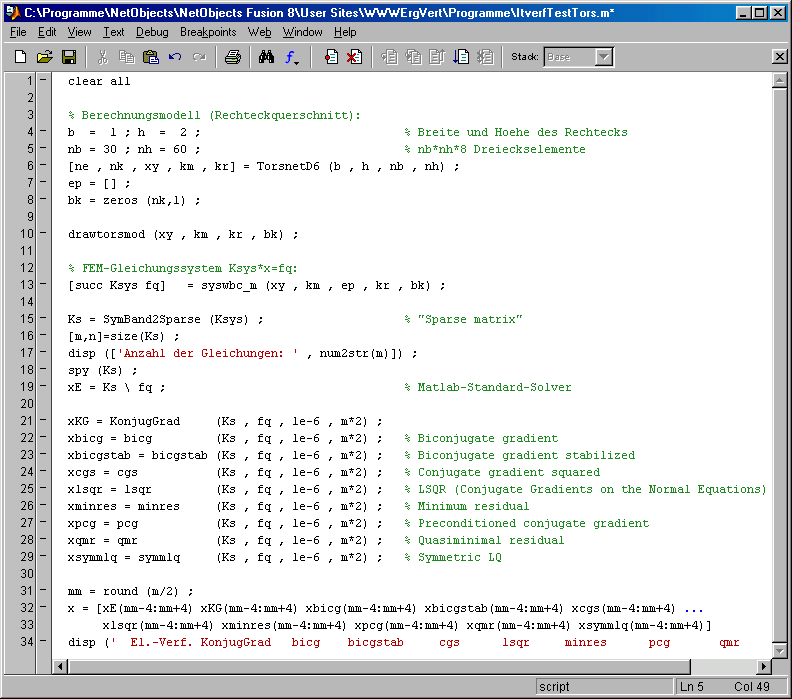
Das oben dargestellte Script baut ein FEM-Modell mit 14400 Elementen auf, so dass ein Gleichungssystem mit 29161 Gleichungen entsteht. Alle iterativen Lösungsverfahren liefern die korrekte Lösung ab. Sie benötigen bis auf eine Ausnahme etwas weniger als 400 Iterationen (nur lsqr ist mit 9533 die einzige Ausnahme). Ausgegeben werden einige Werte etwa aus der Mitte der Lösungsvektoren, die alle die korrekte Lösung bestätigen:
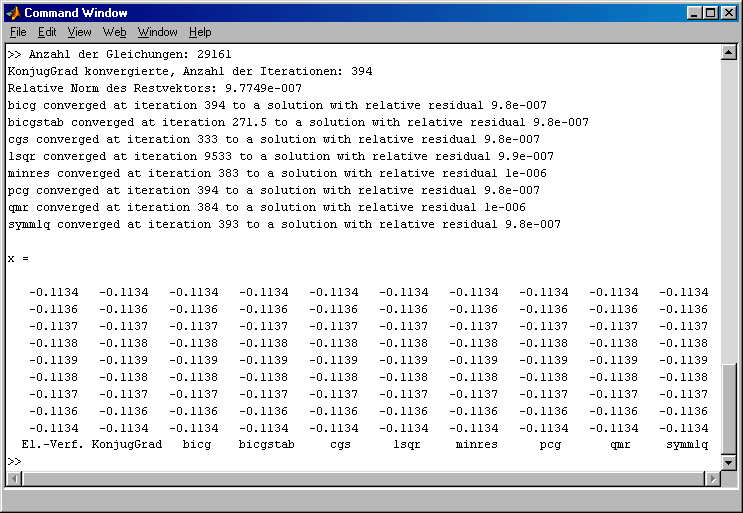
Für dieses Beispiel sind bei beliebiger (mit dem PC noch im Minutenbereich zu erledigender) Gleichungsanzahl die Lösungen mit etwa folgenden erforderlichen Iterationen zu erreichen (hier getestet mit KonjugGrad.m, alle anderen Verfahren außer lsqr liefern etwa gleiche Werte):
|
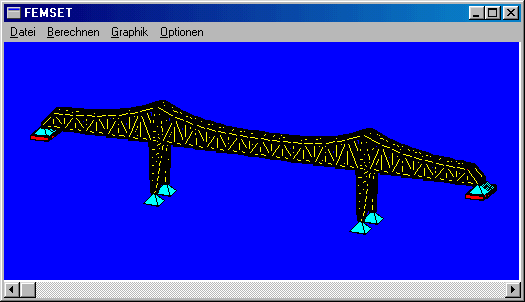
Die nebenstehend zu sehende Brückenkonstruktion wurde mit dreidimensionalen Fachwerkstäben modelliert. Das FEM-Berechnungsmodell ist in der Datei Fof.dat gespeichert und wird im nachfolgenden Matlab-Script eingelesen. Mit Matlab-Femset wird das lineare Gleichungssystem erzeugt, mit dem die Knotenverschiebungen berechnet werden können. Bei 400 Stäben und 136 Knoten ergibt sich ein Gleichungssystem mit 408 Gleichungen. Das Matlab-Script formt die Koeffizientenmatrix in eine "Sparse matrix" um, bevor das Gleichungssystem mit den gleichen Functions wie für das oben dargestellte Torsionsproblem gelöst wird:
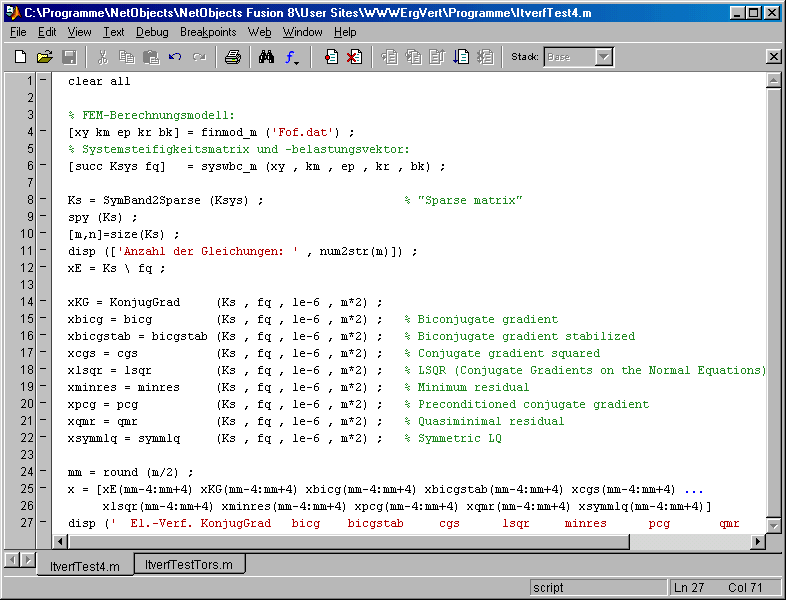
Weil mit den Standardeinstellungen für die Anzahl der maximal auszuführenden Iterationsschritte keines der Verfahren auch nur annähernd brauchbare Ergebnisse lieferte, wurde gleich eine Anzahl erlaubt, die der doppelten Anzahl der Gleichungen entspricht.
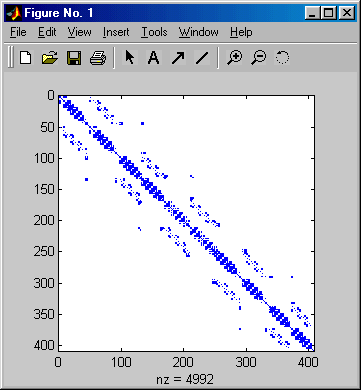
Das Ergebnis der Ausgabe des Musters der von Null verschiedenen Elemente der Koeffizientenmatrix (spy-Function in Zeile 9) ist rechts zu sehen, die Ausgabe der Ergebnisse in das Command Window ist nachfolgend zu sehen.
Alle iterativen Verfahren bis auf lsqr konvergieren und liefern vernünftige Ergebnisse ab. Aber auch das von lsqr abgelieferte Ergebnis liegt schon in der Nähe der richtigen Lösung, so dass angenommen werden kann, dass nach wenigen weiteren Schritten auch hier Konvergenz erreicht worden wäre. Allerdings zeigte dieses Verfahren auch bei den anderen bisher beschriebenen Testrechnungen ein so schlechtes Konvergenzverhalten, dass es für weitere Testrechnungen nicht mehr berücksichtigt wird.
Bei allen übrigen Iterationsverfahren fällt auf, dass die Anzahl der ausgeführten Iterationsschritte bis zur Konvergenz nur um ganz wenige Schritte differiert, so dass zumindest in dieser Hinsicht (und der Aufwand ist ja ein besonders wichtiges Kriterium) keines der Verfahren besonders herausragt.
Dreidimensionales Tragwerk mit biege-, dehn- und torsionssteifen Elementen
Das nebenstehend zu sehende Finite-Elemente-Modell der Brücke über den Nord-Ostsee-Kanal bei Rendsburg besteht aus 1947 Elementen (biege-, dehn- und torsionssteife Träger mit je zwei Knoten), die an 747 Knoten untereinander verbunden sind. Dieses Modell führt auf ein (im Vergleich mit typischen FEM-Modellen eher kleines) Gleichungssystem mit 4482 Unbekannten.
Das FEM-Berechnungsmodell ist in der Datei Rendbrem.dat gespeichert und wird im nachfolgenden Matlab-Script eingelesen. Mit Matlab-Femset wird das lineare Gleichungssystem erzeugt, mit dem die Knotenverschiebungen berechnet werden können.
Das Matlab-Script ItVerfTest5.m formt die Koeffizientenmatrix in eine "Sparse matrix" um. Anschließend wird das Gleichungssystem mit den gleichen Functions (außer lsqr) gelöst, die auch für das oben beschriebene 3D-Fachwerk verwendet wurden:
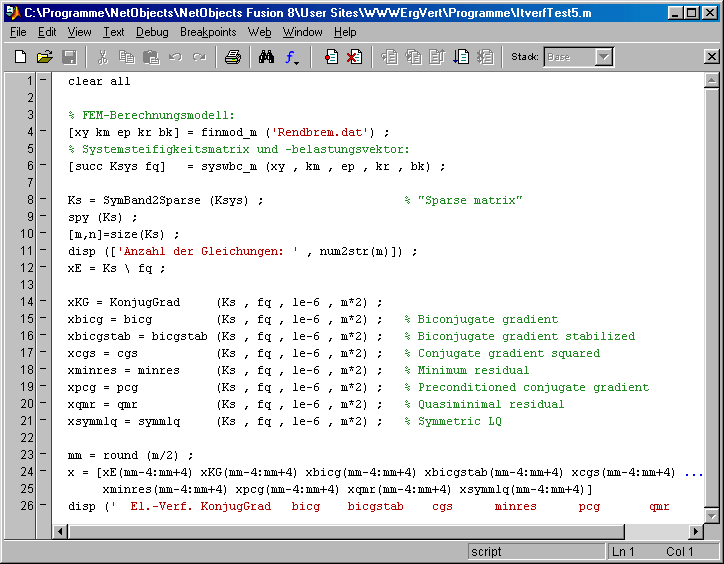
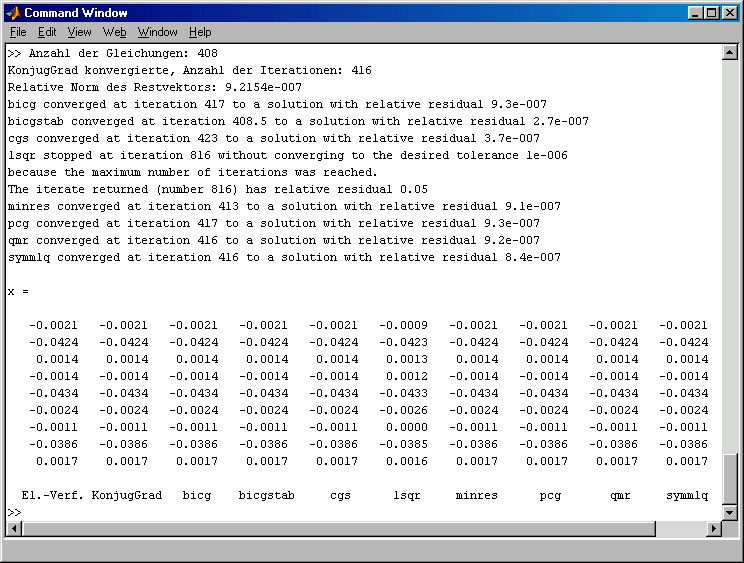
Das Ergebnis der Rechnung ist enttäuschend:
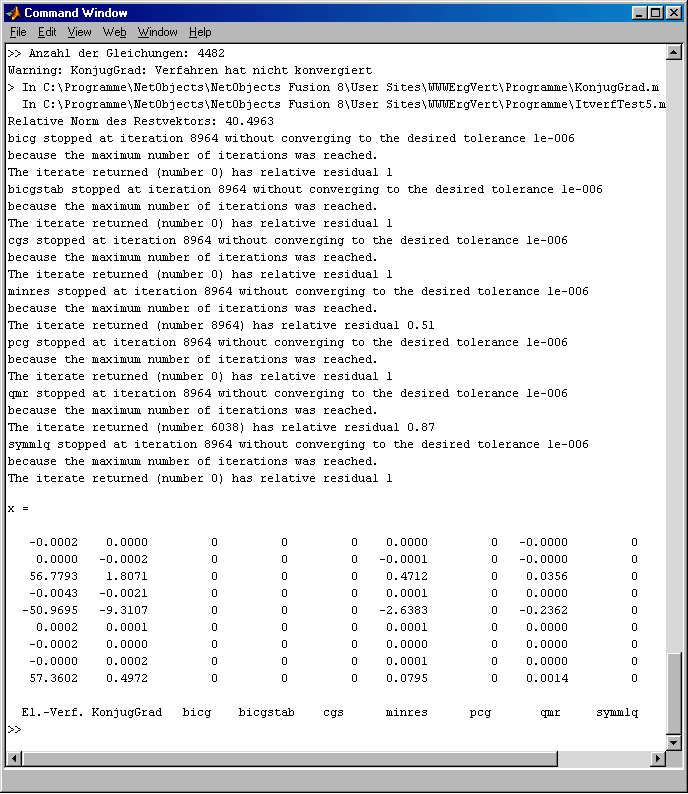
Keines der iterativen Verfahren konvergierte, obwohl 8964 Iterationsschritte zugelassen (und auch ausgeführt) wurden. Die wenigen abgelieferten Ergebnisse sind nicht annähernd im Bereich der Referenzlösung (linke Spalte), die mit dem Matlab-Standard-Solver (Eliminationsverfahren) erzielt wurde. Auch bei 100 000 zugelassenen Iterationen gibt es keine Konvergenz:
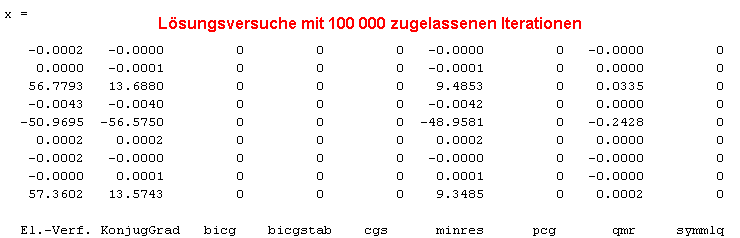
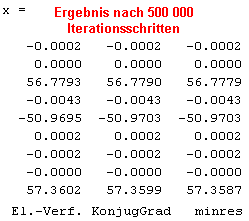Immerhin zeigen zwei Iterationsverfahren eine deutliche Tendenz auf die in der linken Spalte aufgeführten mit einem Eliminationsverfahren erzeugten Lösung. Diesen beiden Verfahren wird noch die Chance zusätzlicher Iterationen gegeben. Nebenstehend ist das Ergebnis zu sehen. Obwohl auch nach 500 000 Iterationen kein Verfahren Konvergenz meldete, sind doch die Ergebnisse der beiden verbliebenen Iterationsverfahren ausreichend gut. Aber der Aufwand ist natürlich nicht akzeptabel.
Bei diesem Beispiel und auch dem kleinen Gleichungssystem mit nur 33 Unbekannten auf der Seite "Testrechnungen für iterative Verfahren (1)" kann der Verdacht aufkommen, dass die Iterationsverfahren nicht konkurrenzfähig sind. Verwiesen wird auf die Möglichkeit der Präkonditionierung, mit der das Konvergenzverhalten verbessert werden kann, und auf die "Testrechnungen mit präkonditioniertem KG-Verfahren" und die "Testrechnungen mit Präkonditionierung mit Matlab", aber auch auf die hier formulierte Warnung.
Download
Die Matlab-Scripts auf dieser Seite und die von ihnen aufgerufenen Functions, DLLs und Dateien sind zum Download verfügbar:
- Die Matlab-Scripts, mit denen die Gleichungssysteme für das Torsionsproblem, das 3D-Fachwerk und das 3D-Rahmentragwerk erzeugt werden, sind als ItverfTestTors.m, ItverfTest4.m und ItverfTest5.m verfügbar.
- Von allen drei Scripts werden die Matlab-Function SymBand2Sparse.m und die DLL syswbc_m.dll aufgerufen.
- Die ebenfalls von allen drei Scripts aufgerufene Function KonjuGrad.m kann von
http://www.mathematik.uni-kassel.de/~meister/buch-online heruntergeladen werden.
- Von ItverfTestTors werden zusätzlich die beiden Functions drawtorsmod.m und TorsnetD6.m aufgerufen.
- Von ItverfTest4.m und ItverfTest5.m wird zusätzlich die DLL finmod_m.dll verwendet.
- IverfTest4.m lädt die FEM-Modell-Datei Fof.dat.
- IverfTest5.m lädt die FEM-Modell-Datei Rendbrem.dat.
