|
Hinweis: Am 18.5.2011 lieferte Herr Dr. Thomas Pieper den Hinweis, dass das auf dieser Seite beschriebene Beispiel in den neueren Matlab-Versionen korrekt gelöst wird. Die unten beschriebene fehlerhafte Lösung wurde mit Matlab 7 (R14) erzeugt. |
|
Das Beispiel
Für den im Bild zu sehenden Biegeträger gelten die folgenden sinnvollen Parameter: l = 1000 mm ; EI = 2 · 1010 Nmm2 ; q0 = 2 N/mm . Der Träger ist - wie unschwer zu erkennen ist - nicht ausreichend gelagert, um tragfähig sein. Eine Finite-Elemente-Berechnung eines solchen Systems führt deshalb auf ein Gleichungssystem mit einer singulären Koeffizientenmatrix. Im folgenden Matlab-Script wird das FEM-Gleichungssystem aufgebaut, die Koeffizientenmatrix wird auf Singularität (Berechnung des Wertes ihrer Determinante) getestet. |
|
Berechnung der Determinante
Die Koeffizientenmatrix wird in Zeile 6 in das Command Window ausgegeben. In Zeile 8 wird ihre Determinante berechnet und ausgegeben. In Zeile 9 wird der Rang der Matrix mit der Matlab-Function rank berechnet und ausgegeben. Die in Zeile 10 aufgerufene Matlab-Function rref erzeugt mit dem Gauß-Jordan-Algorithmus die "reduced row echelon form" der Matrix, die auch den Rang der Matrix erkennen lässt.
Fazit: Die beiden Functions rank und rref erkennen die Singularität der Matrix, det liefert für den Wert der Determinante ein völlig falsches Ergebnis ab. |
|
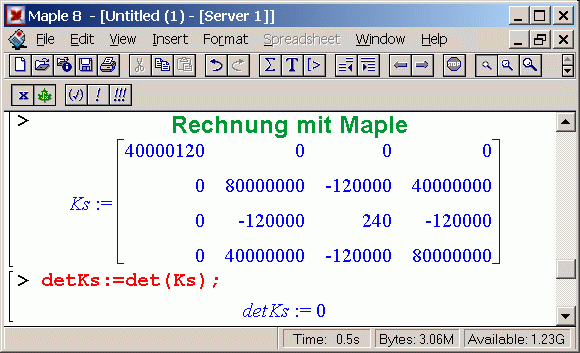

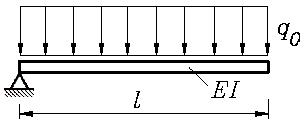 Die Aufgabe, die dem hier beschriebenen Problem zugrunde liegt, ist eigentlich nicht von Interesse. Es soll mit ihr nur gezeigt werden, dass es durchaus kein spitzfindig konstruiertes Problem ist, mit dem die Matrix erzeugt wird, die eine falsche Determinante liefert.
Die Aufgabe, die dem hier beschriebenen Problem zugrunde liegt, ist eigentlich nicht von Interesse. Es soll mit ihr nur gezeigt werden, dass es durchaus kein spitzfindig konstruiertes Problem ist, mit dem die Matrix erzeugt wird, die eine falsche Determinante liefert.
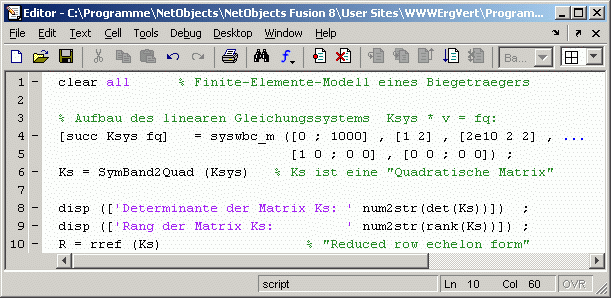 Der Aufbau des Gleichungssystems in den Zeilen 4 bis 6 des nebenstehend zu sehenden Scripts ist für die Betrachtungen hier uninteressant (für Interessenten:
Der Aufbau des Gleichungssystems in den Zeilen 4 bis 6 des nebenstehend zu sehenden Scripts ist für die Betrachtungen hier uninteressant (für Interessenten: 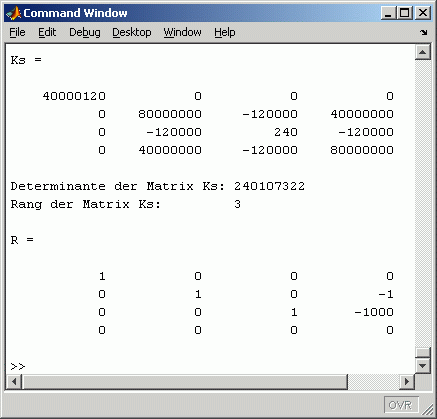 Im Command Window findet man die Ergebnisse der Berechnung:
Im Command Window findet man die Ergebnisse der Berechnung:
