|
Die bequeme Realisierung von Ereignissen
Die nebenstehende Laufkatze mit Last ist dafür ein einfaches Beispiel: Die Antriebskraft F0 wirkt nur für einen kurzen Zeitraum und wird dann abgeschaltet, die Feder hat nur dann eine Wirkung auf die Masse mK, wenn diese Kontakt zu ihr hat. Die Realisierung ist einfach: Man formuliert die Differenzialgleichungen so, als würden Antriebskraft und Federkraft immer wirken, setzt dann aber jeweils die gegebenen Werte für F0 und c bzw. den Wert Null für diese Parameter in Abhängigkeit von der Bewegungssituation. Was bei dieser Aufgabe so schön funktioniert, führt leider manchmal zu Problemen, siehe folgendes Beispiel. |
|
Stillstand ist eine kritische Bewegungssituation
Bei der Formulierung der Differenzialgleichungen muss beachtet werden, dass die auf die Masse wirkende Reibkraft nur im Bereich x > a wirkt und dort ihre Richtung umkehrt, wenn sich die Bewegungsrichtung der Masse umkehrt. Dabei können folgende Situationen eintreten:
Wie reagieren numerische Integrationsverfahren auf eine solche Situation?
In der nebenstehenden Graphik sieht man die Bewegungsgesetze für einen solchen Fall, bei dem nach dem zweiten Wiedereintritt der Masse in den Reibungsbereich die Reibungskraft so groß ist, dass die Federkraft sie nicht mehr überwinden kann: Die Masse bleibt in Ruhe an der erreichten Stelle, die Geschwindigkeit ist ab diesem Zeitpunkt gleich Null. Berechnet wurden diese Diagramme mit einem Runge-Kutta-Verfahren 4. Ordnung mit konstanter Schrittweite, das im Teil 1 des Skripts "Numerische Integration von Anfangswertproblemen" beschrieben wird und zum Download verfügbar ist. Ein scharfer Zoom in das Geschwindigkeits-Zeit-Diagramm (Bild darunter) zeigt, dass es tatsächlich keine saubere Ruhelage ist, sondern eher ein "Wackeln auf der Stelle", was die oben angestellten Überlegungen bestätigt. Aber im Rahmen der von einem numerischen Verfahren zu erwartenden Genauigkeit könnte man mit dieser Situation durchaus zufrieden sein. Diese kritische Situation sollte man also mit den Matlab-ode-Functions nicht eintreten lassen. Diese bieten allerdings mit der nachfolgend beschriebenen "Event-Strategie" eine saubere Lösung an. |
|
Die Event-Strategie der Matlab-ode-Functions Die Matlab-ode-Functions bieten die Möglichkeit, über eine gesondert zu schreibende Function Ereignisse zu definieren und diesen Ereignissen die Optionen "Ereignis nur registrieren und weitermachen" bzw. "Abbruch der Rechnung" zuzuordnen. So kann z. B. in dem oben beschriebenen Beispiel das Ereignis "Geschwindigkeit Null" definiert werden. Die ode-Functions liefern dann alle eingetretenen Ereignisse als zusätzliche Ergebnisse ab (mit dem Zeitpunkt und den Funktionswerten zum Zeitpunkt des Ereignisses). Man kann dies aber auch nutzen, um die oben beschriebene kritische Situation zu entschärfen: Man definiert für dieses Problem den Zustand "Geschwindigkeit gleich Null" als Ereignis, bei dessen Eintreten die Rechnung abgebrochen wird. Dann kann man die vorhandene Situation testen und entscheiden, ob die Rechnung endgültig beendet werden oder weiterlaufen soll. Im letztgenannten Fall wird dann die Rechnung mit den aktuellen Funktionswerten zum Zeitpunkt des Abbruchs als Anfangsbedingungen wieder gestartet. Für diese Aufgabe ergibt sich ein wesentlicher zusätzlicher Vorteil: Man kann den Test beim Stillstand mit dem für die Ruhelage zuständigen Haftungskoeffizienten durchführen (dieser ist in der Regel größer als der für die Bewegung zuständige Gleitreibungskoeffizient). Wie dies realisiert werden kann, wird an dem hier diskutierten Beispiel auf dieser Seite demonstriert. Für die eingangs skizzierte Laufkatze (System mit zwei Freiheitsgraden) findet man die ausführlich beschriebene Lösung auf der Seite "Laufkatze mit pendelnder Last - Berechnung mit der Matlab-Event-Strategie". |

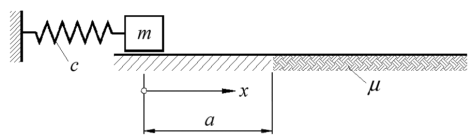 Die Masse in der nebenstehend skizzierten Aufgabe bewegt sich nur im Bereich
Die Masse in der nebenstehend skizzierten Aufgabe bewegt sich nur im Bereich 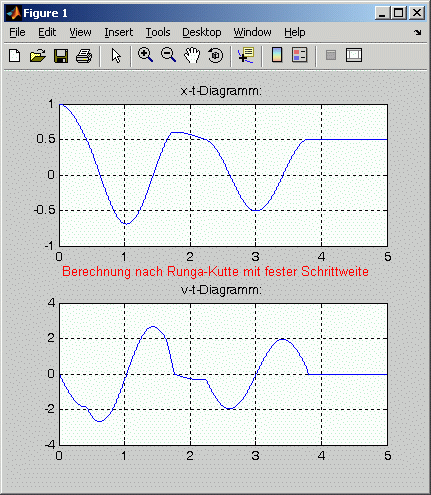 Ein Algorithmus mit fester Schrittweite (und damit festgelegter Anzahl von Integrationsschritten) spielt bis zum Ende des Integrationsintervall genau das beschriebene Spiel mit den ständig wechselnden Richtungen. Bei genügend kleiner Schrittweite sieht die graphische Darstellung der Bewegungsgrößen dann tatsächlich wie Stillstand aus, nachdem die beschriebene Situation eingetreten ist.
Ein Algorithmus mit fester Schrittweite (und damit festgelegter Anzahl von Integrationsschritten) spielt bis zum Ende des Integrationsintervall genau das beschriebene Spiel mit den ständig wechselnden Richtungen. Bei genügend kleiner Schrittweite sieht die graphische Darstellung der Bewegungsgrößen dann tatsächlich wie Stillstand aus, nachdem die beschriebene Situation eingetreten ist.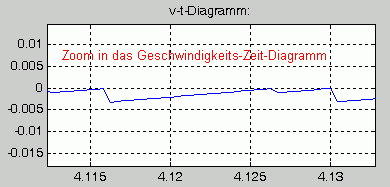 ls wäre die Rechnung in eine Endlos-Schleife geraten, und es bleibt ihm in der Regel nichts anderes übrig, als die Rechnung abzubrechen (und er bekommt dann nicht einmal die bis dahin ermittelten Ergebnisse zu sehen, wenn er nicht die Geduld hat, bei diesem Beispiel mehrere Stunden zu warten, bis ihm ode45 tatsächlich mehr als 3 000 000 Ergebnisse für den Zeitbereich von 5 s liefert).
ls wäre die Rechnung in eine Endlos-Schleife geraten, und es bleibt ihm in der Regel nichts anderes übrig, als die Rechnung abzubrechen (und er bekommt dann nicht einmal die bis dahin ermittelten Ergebnisse zu sehen, wenn er nicht die Geduld hat, bei diesem Beispiel mehrere Stunden zu warten, bis ihm ode45 tatsächlich mehr als 3 000 000 Ergebnisse für den Zeitbereich von 5 s liefert).