|
Das Beispiel
bekannt sein müssen (die Funktion hat unendlich viele Nullstellen). Besonders interessant ist der kleinste von Null verschiedene positive Wert λ1, mit dem die Eigenfrequenz der Grundschwingung berechnet werden kann. Dieser Wert soll nachfolgend ermittelt werden. |
|
Es ist sofort ersichtlich, dass λ = 0 eine Nullstelle der Funktion ist. Diese interessiert nicht. Deshalb wird in dem nachfolgend rechts zu sehenden Matlab-Script folgende Strategie verfolgt:
Das nebenstehend zu sehende Script Nullstelle1.m realisiert diese Berechnung. Nach dem Ermitteln einer Nullstelle wird die Rechnung abgebrochen. Im Command Window findet man das Ergebnis:
Das Ergebnis ist korrekt, wie z. B. auf dieser Seite auch mit mehreren anderen Lösungsverfahren bestätigt wird.
|
|
Vorsicht ist geboten! In älteren Lehrbüchern findet man bei dieser Aufgabe den Hinweis, dass man die nichtlineare Gleichung
durch cosλ coshλ dividieren sollte, so dass die für die Nullstellenberechnung gleichwertige Gleichung
f = tan(lam)-tanh(lam) ; ersetzt, wird die Erwartung, das gleiche Ergebnis wie oben zu erhalten, nicht erfüllt. Man erhält vielmehr das im Command Window rechts zu sehende Ergebnis. Es ist nicht die gesuchte Nullstelle, sondern die durch die tan-Funktion erzeugte Polstelle. Weil es ein ungerader Pol (mit Vorzeichenwechsel) ist, wird auch dieser Punkt von fzero als Ergebnis abgeliefert. Dies ist zumindest verwirrend, entspricht aber der dokumentierten Arbeitsweise von fzero. Man kann sich das über das Anfordern einer erweiterten Ausgabe von fzero bestätigen lassen. Wenn man die Zeile 10 im Script Nullstelle1.m durch [lam1 flam1 exitflag] = fzero (@ewg , lam) ersetzt, erhält man zusätzlich den Funktionswert (für den man an einer Nullstelle einen Wert annähernd Null erwarten kann) und ein exitflag, das eine Aussage über das abgelieferte Ergebnis enthält.
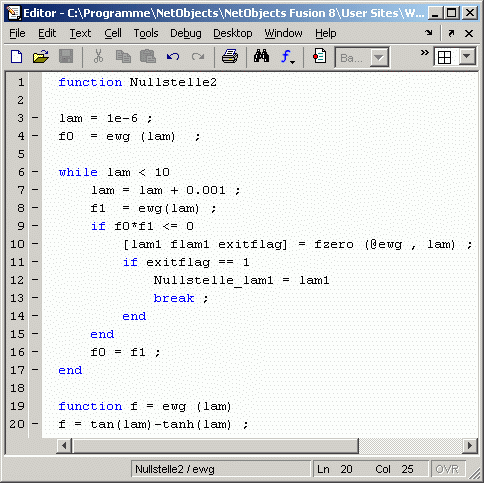
Tatsächlich darf man nur dann eine Nullstelle als Ergebnis von fzero erwarten, wenn das exitflag den Wert 1 hat. Nachfolgend wird deshalb ein Script Nullstelle2.m gezeigt, das dieses exitflag abfragt und nur dann das abgelieferte Ergebnis als Nullstelle akzeptiert (und die Rechnung abbricht), wenn das exitflag dieses tatsächlich als Nullstelle ausweist.
|

 Im Skript "
Im Skript "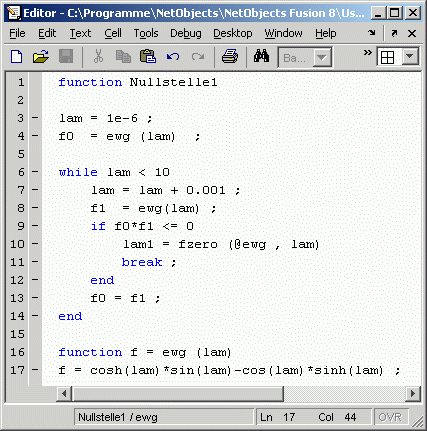 Bei einem Vorzeichenwechsel wird eine Nullstelle in der Nähe des letzten
Bei einem Vorzeichenwechsel wird eine Nullstelle in der Nähe des letzten 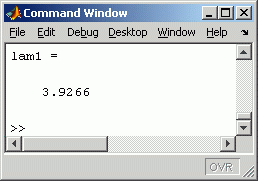
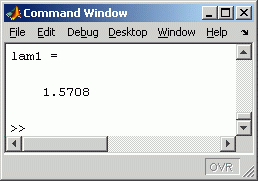 entsteht. Dieser Gleichung sieht man die Lösungen sofort an: Es sind die Schnittpunkte der tan- und der tanh-Funktion. Wenn man nun in dem oben zu sehenden Script die Zeile 17 durch
entsteht. Dieser Gleichung sieht man die Lösungen sofort an: Es sind die Schnittpunkte der tan- und der tanh-Funktion. Wenn man nun in dem oben zu sehenden Script die Zeile 17 durch
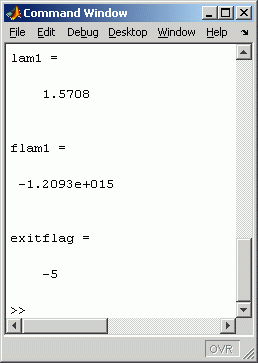 Das nebenstehende Command Window zeigt das Ergebnis dieser Rechnung: Der Funktionswert ist sehr groß (theoretisch müsste er für die berechnete Polstelle -∞ oder +∞ sein). Das exitflag zeigt mit dem Wert -5 laut Matlab-Hilfe: "fzero might have converged to a singular point."
Das nebenstehende Command Window zeigt das Ergebnis dieser Rechnung: Der Funktionswert ist sehr groß (theoretisch müsste er für die berechnete Polstelle -∞ oder +∞ sein). Das exitflag zeigt mit dem Wert -5 laut Matlab-Hilfe: "fzero might have converged to a singular point."