|
Die Aufgabe
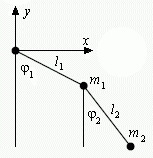
Ein einfaches Doppelpendel besteht aus zwei Punktmassen, die mit masselosen starren Stangen verbunden sind, keine Reibung, kein Luftwiderstand). Die Differenzialgleichungen werden am Ende des Kapitels 7 hergeleitet:
Die Masse m2 wird an einen durch die Koordinaten im x-y-System zu beschreibenden Punkt geführt, und das System wird danach ohne Anfangsgeschwindigkeiten freigelassen. |
|
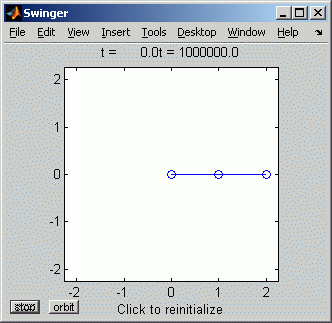
Das Function-Script swinger.m Die in dem Buch von Cleve Moler beschriebenen Matlab-Scripts stehen unter http://www.mathworks.com/moler/ncmfilelist.html) zum Download zur Verfügung. Für das hier betrachtete Doppelpendel heißt die Datei swinger.m, ein ansehenswertes Script, das u. a. zeigt, wie man parallel zur Abarbeitung der ode-Functions die Zwischenergebnisse verarbeiten kann, in dem man z. B. eine Animation des Bewegungsablaufs erzeugt. Im Script swinger.m erhalten alle Problemparameter (m1, m2, l1, l2, g) den Wert 1, so das sich für t keine der vertrauten Dimensionen für die Zeit ergibt, aber das ist für die Betrachtungen hier unerheblich. Das t-Intervall, für das die Lösung erzeugt wird, ist praktisch unendlich groß (obere Grenze: 106), so dass die Bewegung solange läuft, bis der Benutzer den Stop-Button anklickt.
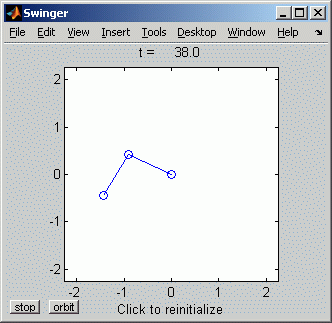
Das Script kann mit Angabe dieser beiden Koordinaten aus dem Command Window mit swinger(2,0) gestartet werden, und man sieht im Graphik-Window die Animation der Bewegung (rechts ein Schnappschuss bei t = 38). Die Animation läuft bis zum Abbruch durch den Benutzer. Die Frage ist, wie lange die dargestellte Bewegung tatsächlich das in der Aufgabenstellung formulierte Problem abbildet. |
|
Wie lange stimmt die Rechnung?
In den Zeilen 20 und 21 werden die Funktionen φ1(t) und φ2(t) für beide Rechnungen in jeweils einem Graphik-Fenster dargestellt (die "Original-swinger-Rechnung" in rot, die "genauere Rechnung" in blau).
Die Abweichungen sind von den gewählten Anfangsbedingungen abhängig, bei einigen Anfangsbedingungen liefen die beiden Kurven schon wesentlich eher auseinander, bei anderen (kleinen) Anfangsausschlägen überdeckten sie sich im gesamten hier betrachteten Bereich. Fazit: Auch die Vorsichtsmaßnahme mit dem MaxStep-Wert 0,05 in swinger.m genügt nicht, um über einen längeren Zeitbereich brauchbare Lösungen zu erzeugen. Man beachte vor allen Dingen, dass die Rechnung weder abstürzt noch irgendwelche Anzeichen dafür liefert, dass die Ergebnisse nichts mehr mit der Aufgabenstellung zu tun haben. Die Animation in swinger.m würde sogar bis t = 106 hübsch anzusehen sein (wie übrigens auch eine korrekte Lösung, wenn man sie denn erzeugen könnte). |
|
Vorstellbare Parameter, Zeit in Sekunden
Man muss also nur die Zeile 32 in der Function swinger1 in g = 9.81 ; ändern, um ein Doppelpendel mit folgenden Parametern zu berechnen: m1 = m2 = 1 kg ; l1 = l2 = 1 m ; g = 9,81 m/s2 . Rechts sieht man das Ergebnis dieser Rechnung: Schon nach etwa 10 Sekunden laufen die beiden Kurven auseinander, was nicht einmal heißt, dass die genauere Rechung richtig ist. Tatsächlich sind ab etwa t = 12 s beide Lösungen falsch. |
Der Vorwurf wird akzeptiert, ...
... dass das Doppelpendel mit seiner chaotischen Bewegung natürlich ein besonders gemeines Objekt für den Test der Genauigkeit der Ergebnisse von Verfahren für die numerische Integration von Anfangswertproblemen ist.
Andererseits ...
- ... ist das Doppelpendel besonders geeignet, um auf die Probleme aufmerksam zu machen, die bei anderen Aufgabenstellungen auch (wenn auch später) auftauchen (und ohne Mehrfachrechnung kommt man eigentlich niemals aus), und ...
- ... es sollte eine Warnung sein, dass man aus der Tatsache, dass man einen Bewegungsablauf auch über einen längeren Zeitraum simulieren und mit einer Animation sehr schön veranschaulichen kann, nicht schließen darf, dass die zu sehende Bewegung (zumindest ab einem gewissen Zeitpunkt) tatsächlich etwas mit der Aufgabenstellung zu tun hat.
|
Physikalisches Doppelpendel Die ausführliche Analyse eines physikalischen Doppelpendels (zwei starre Körper, keine Punktmassen, Differenzialgleichungen gleichen Typs, nur etwas komplizierter) findet man in den Kapiteln "Prinzipien der Mechanik" und "Verifizieren von Computerrechnungen". Die Berechnung mit unterschiedlichen Verfahren und unterschiedlichen Programmen findet man über die Seite "Doppelpendel mit großen Ausschlägen". Auf der Seite "Doppelpendel - Grenzen der Simulation" werden für dieses Problem die zeitlichen Grenzen ausgelotet, für die eine Simulation sinnvoll ist. Dort wird auch gezeigt, warum ein "Dauerläufer", wie er nebenstehend zu sehen ist, ganz gewiss nicht auf einer seriösen Berechnung beruhen kann. |
Ein "Dauerläufer" ist in jedem Fall geschummelt. Hier
wird ein "Animated GIF" immer wieder abgespielt:
|
Abschließende Bemerkung
Keiner der Sätze auf dieser Seite sollte als Kritik verstanden werden, im Gegenteil: Matlab stellt eine gelungene Auswahl sehr effektiver Verfahren für die numerische Integration von Anfangswertproblemen zur Verfügung, die zweifelsfrei sehr gut implementiert wurden. Die Probleme sind einfach schwierig, weil
- einerseits bei Aufgaben dieser Art alle kritischen Situationen der numerischen Rechnung gleichzeitig auftreten können und
- andererseits keine Alternative zur numerischen Lösung zur Verfügung steht.

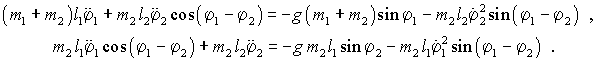
 Die Anfangslage wird durch die Koordinaten der Masse
Die Anfangslage wird durch die Koordinaten der Masse 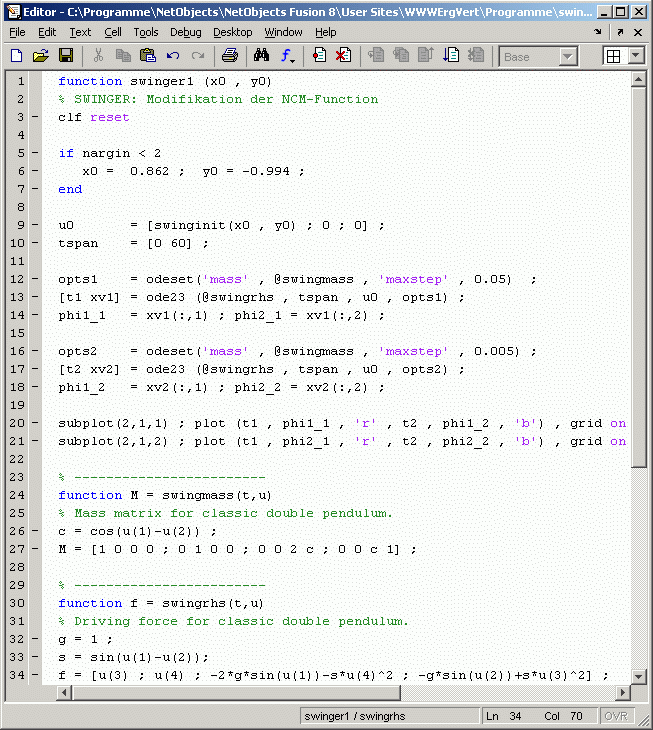 Zur Untersuchung dieser Frage wird (unter Beibehaltung aller wesentlichen Passagen des Scripts swinger.m) ein vereinfachtes Script swinger1.m erzeugt (nebenstehend sind die wesentlichen Passagen dieses Scripts zu sehen). Dieses verzichtet auf die Animation zugunsten der graphischen Darstellung der Bewegungsgesetze
Zur Untersuchung dieser Frage wird (unter Beibehaltung aller wesentlichen Passagen des Scripts swinger.m) ein vereinfachtes Script swinger1.m erzeugt (nebenstehend sind die wesentlichen Passagen dieses Scripts zu sehen). Dieses verzichtet auf die Animation zugunsten der graphischen Darstellung der Bewegungsgesetze 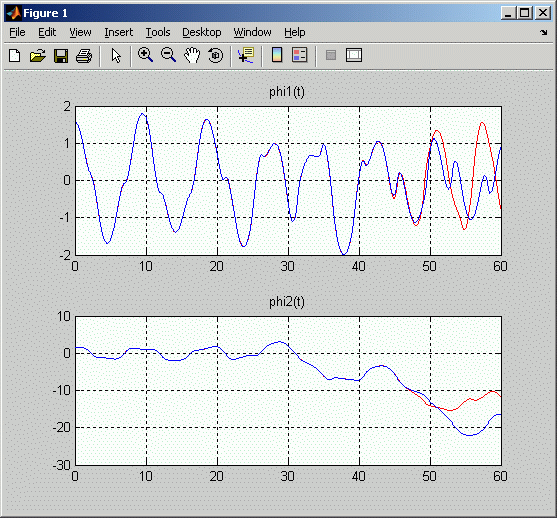 Die nebenstehende Graphik zeigt das Ergebnis. Am Anfang überdecken sich die beiden Kurven, aber ab etwa
Die nebenstehende Graphik zeigt das Ergebnis. Am Anfang überdecken sich die beiden Kurven, aber ab etwa 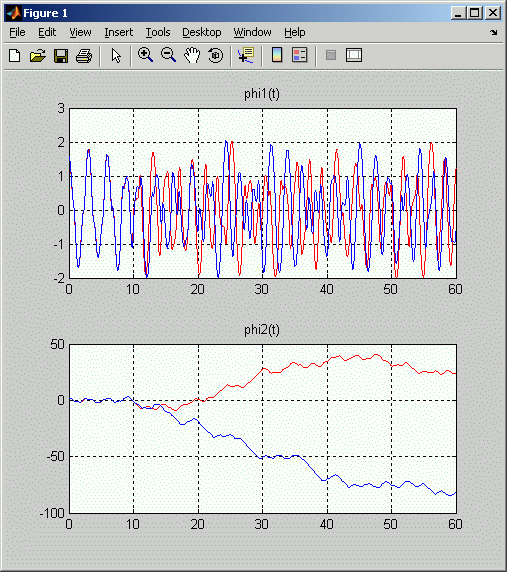 Weil das swinger-Beispiel mit Einheitswerten arbeitet, soll hier noch eine Vorstellung davon gegeben werden, wie groß der Zeitbereich tatsächlich ist, in dem brauchbare Lösungen geliefert werden. Dazu muss nur ein Parameter geändert werden, denn man kann sich für die Einheitswerte der Massen und der Längen vorstellen, dass sie in kg bzw. m zu interpretieren sind. Wenn man dann für
Weil das swinger-Beispiel mit Einheitswerten arbeitet, soll hier noch eine Vorstellung davon gegeben werden, wie groß der Zeitbereich tatsächlich ist, in dem brauchbare Lösungen geliefert werden. Dazu muss nur ein Parameter geändert werden, denn man kann sich für die Einheitswerte der Massen und der Längen vorstellen, dass sie in kg bzw. m zu interpretieren sind. Wenn man dann für 