|
Das Problem Ein lineares Gleichungssystem mit quadratischer Koeffizientenmatrix (n Gleichungen mit n Unbekannten)
hat nur dann eine eindeutige Lösung, wenn die Koeffizientenmatrix nicht singulär ist. Bei Ingenieurproblemen, die durch lineare Gleichungssysteme beschrieben werden, deutet Singularität z. B. auf eine nicht tragfähige Konstruktion hin, der häufigste Fall sind aber einfach Fehler, die beim Aufstellen des Gleichungssystems passieren. In jedem Fall ist das Erkennen der Singularität beim Versuch, das Gleichungssystem zu lösen, eine ganz wichtige Information für den Anwender. Wegen der unvermeidlichen Rundungsfehler bei der Computerrechnung kann eigentlich Singularität nie sicher erkannt, sondern immer nur vermutet werden, vgl. z. B .: "Schwieriges Problem: Singularität erkennen". Aber der Anwender vertraut natürlich darauf, dass im Falle singulärer Matrix wenigstens eine Warnung (auf der Basis der "Vermutung") generiert wird. Ein besonders kritischer Fall tritt dann ein, wenn (ohne Warnung) einfach unsinnige Ergebnisse abgeliefert werden. Dass dieser Fall eintreten kann, wird nachfolgend an einem Beispiel gezeigt, weitere Beispiele dazu findet man unter "Matlab: Probleme mit singulären Matrizen (1)" und "Matlab: Probleme mit singulären Matrizen (2)". |
|
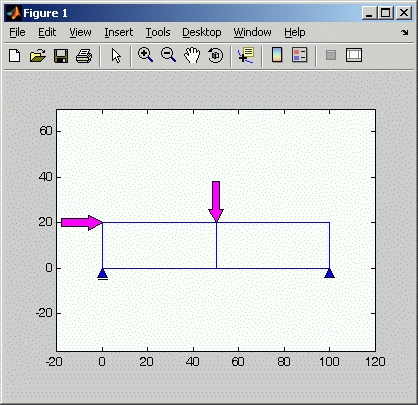
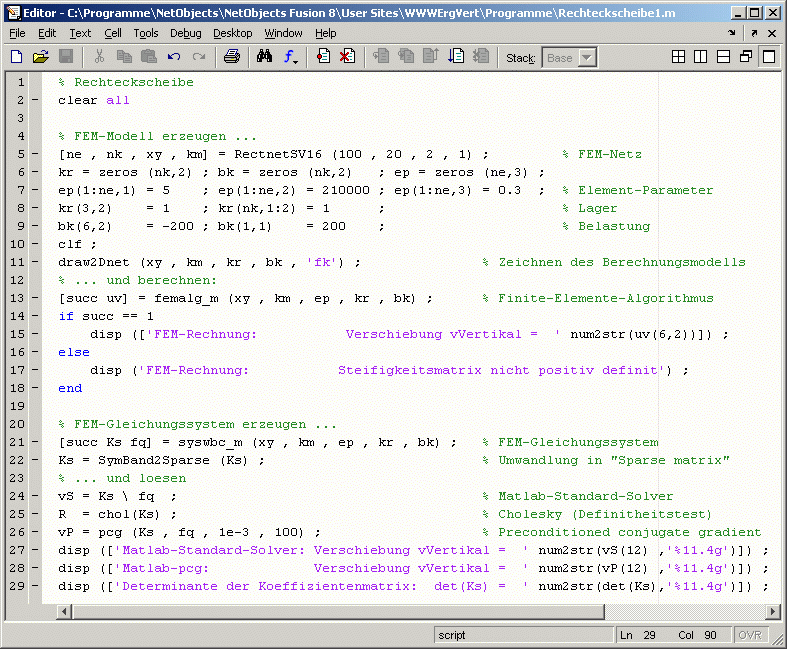
Auch wenn die Herkunft des betrachteten Gleichungssystems für die hier angestellten Überlegungen keine Rolle spielt, sollen doch wenigstens einige Informationen über das behandelte Berechnungsmodell gegeben werden: Es wird ein einfaches Finite-Elemente-Modell aufgebaut (die nebenstehend zu sehende ebene Scheibe). Es ist eine ebene Scheibe, diskretisiert mit nur zwei finiten Elementen (8-Knoten-Scheiben-Vierecke, für Interessenten: Matlab-Femset). Das System ist mit zwei Kräften belastet und ausreichend gelagert (Verschiebungen in beiden Richtungen am Knoten unten rechts verhindert und verhinderte Vertikalverschiebung am Knoten unten links). In der skizzierten Variante ist es also ein tragfähiges und korrekt modelliertes System. Der Finite-Elemente-Algorithmus erzeugt für dieses System ein lineares Gleichungssystem mit 26 Gleichungen. Die Koeffizientenmatrix des Gleichungssystems (Steifigkeitsmatrix) ist symmetrisch und positiv definit. Im nachfolgend zu sehenden Matlab-Script wird das FEM-Modell in den Zeilen 5 bis 9 aufgebaut und in Zeile 13 gelöst. Anschließend wird noch einmal (Zeilen 21 und 22) nur das lineare Gleichungssystem erzeugt und verschiedenen Matlab-Solvern zur Lösung übergeben.
|
|
Ein typischer Fehler bei Finite-Elemente-Berechnungen ist die falsche Modellierung der Lagerung. Wenn man versehentlich in dem oben zu sehenden Script in Zeile 8 nur eine Ziffer ändert und kr(3,1) = 1 ; an Stelle von kr(3,2) = 1 ; schreibt, dann bedeutet das, dass das linke Lager nicht mehr die vertikale, sondern die horizontale Verschiebung verhindert (nebenstehende Graphik). Solch ein Fehler ist typisch auch für die interaktive Erzeugung von Finite-Elemente-Modellen über die Benutzer-Oberfläche von FEM-Programmsystemen. Dieses (nun falsche) Modell beschreibt eine nicht tragfähige Konstruktion, denn es sind unendlich kleine Starrkörper-Drehungen um das rechte Lager möglich. Für die Generierung des Finite-Elemente-Modells bedeutet das, dass ein lineares Gleichungssystem mit singulärer (und damit auch nicht mehr positiv definiter) Koeffizientenmatrix entsteht. Der Anwender darf hoffen, dass er auf die Fehlerhaftigkeit seines Modells bei der versuchten Lösung des Gleichungssystems aufmerksam gemacht wird. Es ist für ihn schon schlimm genug, dass er in der Regel nicht die Ursache, sondern nur eine Meldung wie "Steifigkeitsmatrix ist nicht positiv definit" erfährt, aber wenigstens dieses Indiz erwartet er.
|
|
Abschließende Bemerkungen
Beide Reaktionen sind angemessen.
|
|
Zum Download verfügbar sind
|

 Das Beispiel
Das Beispiel
 Im nebenstehenden Command Window sind die Ergebnisse der erfolgreichen Rechnung zu sehen:
Im nebenstehenden Command Window sind die Ergebnisse der erfolgreichen Rechnung zu sehen:
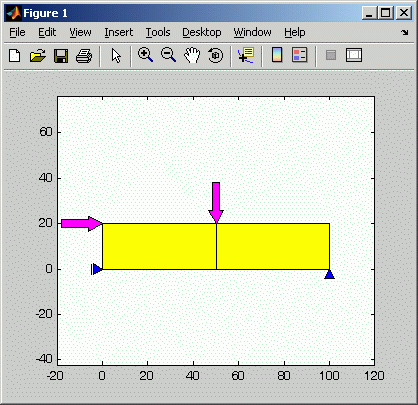 Der kleine Fehler und die Folgen
Der kleine Fehler und die Folgen
 Nebenstehend ist das Command Window mit den Ergebnissen dieser Rechnung zu sehen:
Nebenstehend ist das Command Window mit den Ergebnissen dieser Rechnung zu sehen:
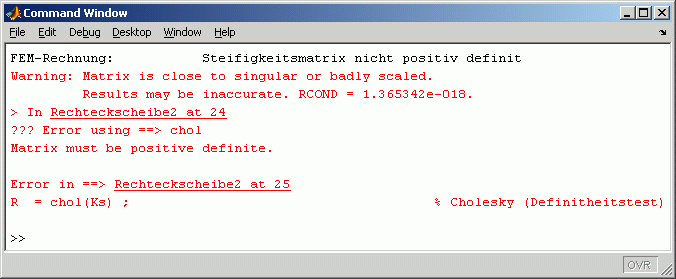 Das hier demonstrierte Verhalten der Matlab-Solver bei singulärer Koeffizientenmatrix ist kein Einzelfall. Vornehmlich (aber durchaus nicht ausschließlich) kommt es zu diesem Verhalten bei Benutzung des
Das hier demonstrierte Verhalten der Matlab-Solver bei singulärer Koeffizientenmatrix ist kein Einzelfall. Vornehmlich (aber durchaus nicht ausschließlich) kommt es zu diesem Verhalten bei Benutzung des 