Das Problem
Eine quadratische Matrix ist singulär, wenn die ihr zugeordnete Determinante den Wert Null hat. Lineare Gleichungssysteme mit singulärer Koeffizientenmatrix sind nicht oder nicht eindeutig lösbar. Der Aufwand für die Berechnung einer Determinante entspricht etwa dem Aufwand zur Lösung eines linearen Gleichungssystems. Deshalb wird die Prüfung auf Singularität der Koeffizientenmatrix (und damit Lösbarkeit des Gleichungssystems) im Allgemeinen nicht gesondert durchgeführt, sondern von den Lösungsverfahren erledigt (z. B. beim Gauß-Algorithmus durch Prüfung der Pivot-Elemente).
Weil während der Berechnung die unvermeidlichen Rundungsfehler hinzukommen, ist immer nur eine Aussage in der Art "fast singulär" oder "sehr schlecht konditioniert" möglich. Beim Gauß-Algorithmus z. B. wird normalerweise keine Null als Pivot-Element entstehen (was theoretisch bei singulärer Matrix geschehen müsste), es kann deshalb nur "bei sehr kleinem Pivot Singularität vermutet werden".
Das nachfolgende kleine Beispiel demonstriert dieses Problem mit Matlab.
Beispiel 1 (widerspruchsfreies System)
Das Gleichungssystem
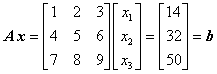
hat eine singuläre Koeffizientenmatrix. Es wird auf der Seite "Lösbarkeit linearer Gleichungssysteme" ausführlich behandelt. Dort wird auch gezeigt, dass es keinen Widerspruch enthält (Rang der Koeffizientenmatrix ist gleich dem Rang der erweiterten Matrix, für beide gilt: r = 2).
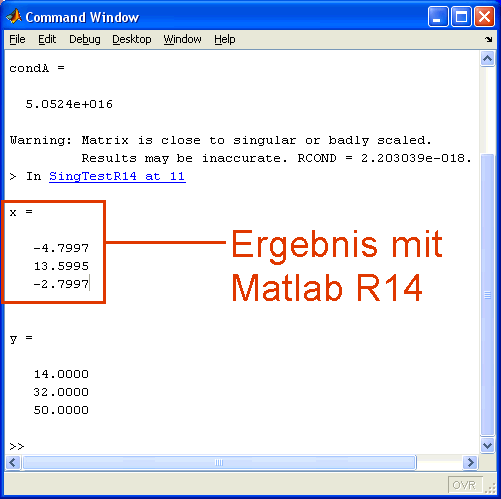 Das nachfolgend zu sehende kleine Matlab-Script versucht, dieses Gleichungssystem mit dem Matlab-Standard-Solver zu lösen.
Das nachfolgend zu sehende kleine Matlab-Script versucht, dieses Gleichungssystem mit dem Matlab-Standard-Solver zu lösen.
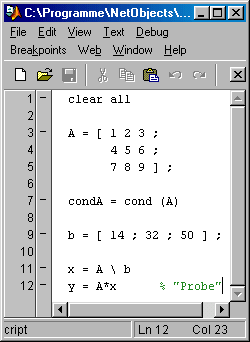
Der nebenstehende Schnappschuss des Command Windows zeigt das Ergebnis (mit Matlab R14). Die Formulierung der Warnung bestätigt, dass aus den oben genannten Gründen die Singularität nur vermutet werden kann. Es wird trotzdem ein (korrektes) Ergebnis ausgewiesen (die durch "Einsetzen" des Ergebnisses in das Ausgangssystem durchgeführte "Probe" bestätigt die Richtigkeit).
 Aber: Es ist natürlich nicht die Lösung des Gleichungssystems, sondern nur eine von unendlich vielen. Bei einer Rechnung unter Verwendung von Matlab R13 ergibt sich eine ganz andere (aber auch richtige) Lösung. Ein Vergleich mit der allgemeinen Lösung (und die jeweils erfolgreiche "Probe durch Einsetzen") zeigt in beiden Fällen die Richtigkeit der ausgegebenen speziellen Lösungen.
Aber: Es ist natürlich nicht die Lösung des Gleichungssystems, sondern nur eine von unendlich vielen. Bei einer Rechnung unter Verwendung von Matlab R13 ergibt sich eine ganz andere (aber auch richtige) Lösung. Ein Vergleich mit der allgemeinen Lösung (und die jeweils erfolgreiche "Probe durch Einsetzen") zeigt in beiden Fällen die Richtigkeit der ausgegebenen speziellen Lösungen.
Die Konditionszahl der Matrix hat einen sehr großen Wert (theoretisch müsste sie für die singuläre Matrix unendlich sein).
Nur bei ganz kleinen Matrizen ist die Aussage zur Singularität deutlicher:
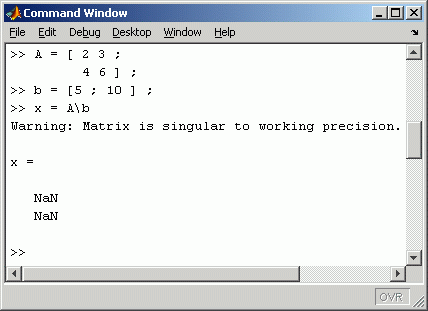
Hier wurde (direkt im Command Window) versucht, das Gleichungssystem
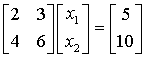
zu lösen. Man sollte nach den gerade gemachten Erfahrungen eigentlich erwarten, dass eine Lösung abgeliefert wird, denn dieses System hat (wie das System oben) zwar eine singuläre Koeffizientenmatrix, enthält aber auch keinen Widerspruch (z. B. ist x1 = x2 = 1 eine Lösung). Bei dieser schärferen Formulierung zur Singularität wird aber keine Lösung abgeliefert (NaN steht in Matlab für "Not a Number").
Beispiel 2 (nicht widerspruchsfreies System)
Für das gegenüber Beispiel 1 nur auf der rechten Seite leicht modifizierte Gleichungssystem
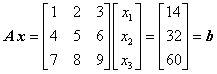
gilt: Koeffizientenmatrix ist singulär mit Rang r = 2, und der Rang der erweiterten Koeffizientenmatrix ist größer. Deshalb hat dieses Gleichungssystem keine Lösung (in den Gleichungen stecken Widersprüche, vgl. die Diskussion dieses Gleichungssystems hier).
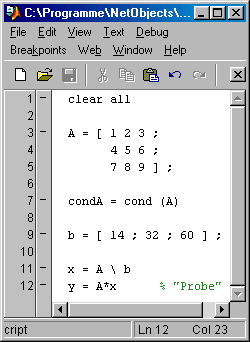
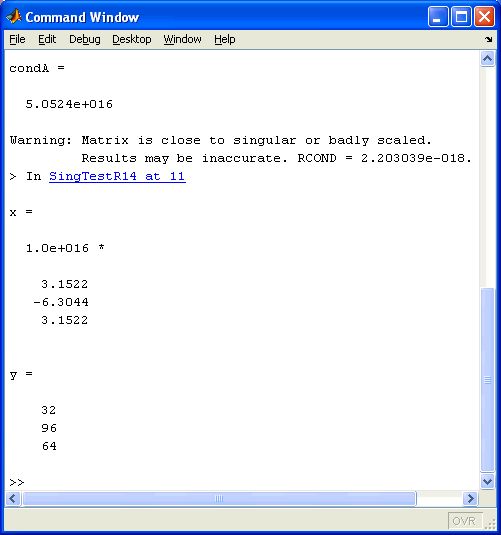 Das nachfolgend zu sehende Matlab-Script liefert (mit Matlab R14) die nebenstehend zu sehenden Ergebnisse ab.
Das nachfolgend zu sehende Matlab-Script liefert (mit Matlab R14) die nebenstehend zu sehenden Ergebnisse ab.
Auch der der Hinweis "Results may be inaccurate" trifft in diesem Fall nicht zu. Sie sind nicht ungenau, sie können nicht einmal falsch sein, denn dieses Gleichungssystem hat gar keine Lösung. Die Größenordnung der Elemente des ausgegebenen Vektors x ist natürlich schon verdächtig. Es ist allerdings überraschend, dass bei diesen Werten die Multiplikation Ax solche glatten (aber falschen) Werte liefert.
Fazit
Weil eingangs die Schwierigkeiten, Singularität zu erkennen, geschildert wurden, soll die Kritik am Verhalten Matlabs moderat ausfallen, in jedem Fall ist aber Vorsicht geboten. Die ausgewiesene Konditonszahl ist ein Hinweis darauf, dass die Ergebnisse nicht nur falsch sein können, sondern unter Umständen gar keine Ergebisse der Aufgabenstellung sind. Sicher wäre es besser, wenn Matlab bei solchen Konditionszahlen gar kein Ergebnis abliefern würde (vgl. hierzu: "Matlab: Probleme mit singulären Matrizen").

