Beispiel
 Die Methode der finiten Elemente führt in der Regel auf lineare Gleichungssysteme mit symmetrischen, positiv definiten Koeffizientenmatrizen, die gut konditioniert sind. Diese Aussage muss relativiert werden für Probleme, bei denen z. B. unterschiedliche Steifigkeiten dazu führen, dass auch auf der Hauptdiagonalen der Koeffizientenmatrix Elemente mit stark unterschiedlicher Größe stehen (typisch u. a. für Rahmentragwerke, bei denen Biege- und Dehnsteifigkeiten zu berücksichtigen sind, oder bei Schalen, bei Faltwerken mit Membran- und Biegespannungen, aber auch bei Kontinua mit orthotropen Materialeigenschaften).
Die Methode der finiten Elemente führt in der Regel auf lineare Gleichungssysteme mit symmetrischen, positiv definiten Koeffizientenmatrizen, die gut konditioniert sind. Diese Aussage muss relativiert werden für Probleme, bei denen z. B. unterschiedliche Steifigkeiten dazu führen, dass auch auf der Hauptdiagonalen der Koeffizientenmatrix Elemente mit stark unterschiedlicher Größe stehen (typisch u. a. für Rahmentragwerke, bei denen Biege- und Dehnsteifigkeiten zu berücksichtigen sind, oder bei Schalen, bei Faltwerken mit Membran- und Biegespannungen, aber auch bei Kontinua mit orthotropen Materialeigenschaften).
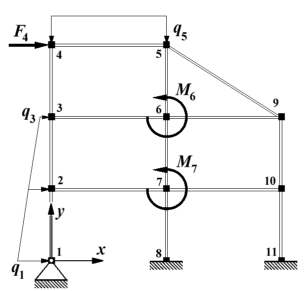
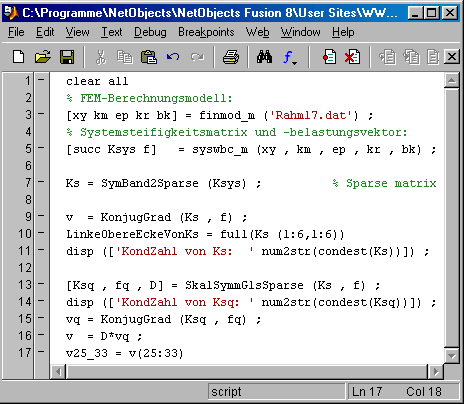
Dass gerade in solchen Fällen die Skalierung eine erhebliche Verbesserung der Kondition der Koeffizientenmatrix bringen kann, soll hier an einem ganz kleinen Beispiel gezeigt werden. Nachstehend ist der ebene biege- und dehnsteife Rahmen dargestellt (Aufgabe aus dem Kapitel "Verifizieren von Computerrechnungen"), dessen FEM-Modell in der Datei Rahm17.dat gespeichert ist. Diese wird im nachfolgend zu sehenden Script in Zeile 3 geladen, in Zeile 5 wird mit Matlab-Femset das lineare Gleichungssystem aufgebaut, das für dieses Problem nur 33 Gleichungen hat.
In Zeile 7 wird die Koeffizientenmatrix in das von Matlab unterstützte "Sparse matrix"-Format umgewandelt. Um die Auswirkungen der schlechten Kondition der Koeffizientenmatrix zu demonstrieren, wird in Zeile 9 zunächst die Lösung des Gleichungssystems mit dem Konjugierte-Gradienten-Verfahren versucht. Dafür wird die auch für andere Testrechnungen benutzte Matlab-Function KonjugGrad.m verwendet (aus dem Anhang des Buchs "A. Meister: Numerik linearer Gleichungssysteme", über den Link http://www.mathematik.uni-kassel.de/~meister/buch_online zum Download verfügbar).
 Die Lösung misslingt (siehe das unten zu sehende Command window), und mit den Ausgaben in Zeilen 10 und 11 werden die Gründe dafür deutlich: Schon auf dem Ausschnitt der Matrix (linke obere Ecke) sieht man, dass sich die Elemente auf der Hauptdigonalen in der Größenordnung um 5 Zehnerpotenzen unterscheiden. Der recht große Wert für die Konditionszahl (größer als 108) bestätigt die schlechte Kondition.
Die Lösung misslingt (siehe das unten zu sehende Command window), und mit den Ausgaben in Zeilen 10 und 11 werden die Gründe dafür deutlich: Schon auf dem Ausschnitt der Matrix (linke obere Ecke) sieht man, dass sich die Elemente auf der Hauptdigonalen in der Größenordnung um 5 Zehnerpotenzen unterscheiden. Der recht große Wert für die Konditionszahl (größer als 108) bestätigt die schlechte Kondition.
Die in der Zeile 13 aufgerufene Function führt die Skalierung mit dem hier beschriebenen Algorithmus aus: Die Koeffizientenmatrix wird sowohl von rechts als auch von links mit einer Diagonalmatrix multipliziert, die die reziproken Werte der Quadratwurzeln der Diagonalelemente der Koeffizientenmatrix enthält, der Vektor der rechten Seite wird von links mit dieser Diagonalmatrix multipliziert. Unter Erhalt der Symmetrie bekommenen auf diesem Wege alle Diagonalelemente den Wert 1. Die Ausgabe in Zeile 14 bestätigt die deutliche Verbesserung der Konditionszahl auf den Wert 2586.
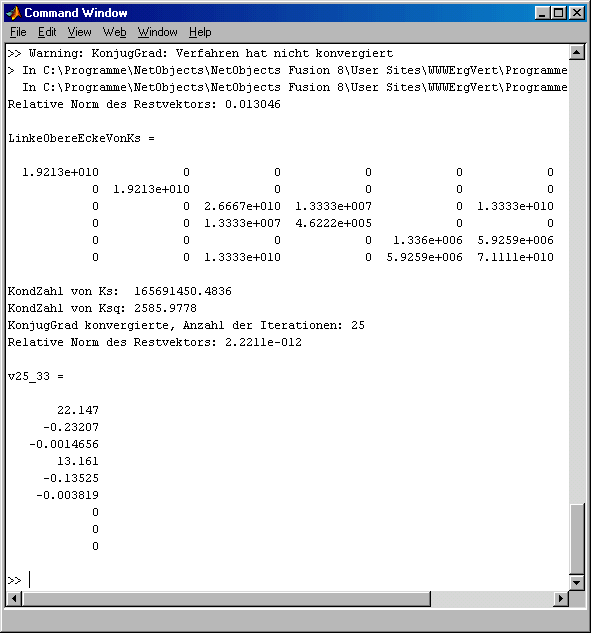 Der erneute Versuch, das nun transformierte Gleichungssystem zu lösen, hat Erfolg. Das Ergebnis muss noch rücktransformiert werden (Zeile 16). In Zeile 17 werden nur einige Elemente des Lösungsvektors ausgegeben. Ein Vergleich mit den Ergebnissen, die mit anderen Verfahren ermittelt wurden, bestätigt die Richtigkeit.
Der erneute Versuch, das nun transformierte Gleichungssystem zu lösen, hat Erfolg. Das Ergebnis muss noch rücktransformiert werden (Zeile 16). In Zeile 17 werden nur einige Elemente des Lösungsvektors ausgegeben. Ein Vergleich mit den Ergebnissen, die mit anderen Verfahren ermittelt wurden, bestätigt die Richtigkeit.
Zum Download verfügbar sind das abgebildete Matlab-Script und die daraus aufgerufenen Functions und DLLs:
SkalTest1.m, finmod_.dll, syswbc_m.dll, SymBand2Sparse.m, SkalSymmGlsSparse.m, das FEM-Modell
befindet sich in der Datei Rahm17.dat. Die Matlab-Function KonjugGrad.m steht über den
Link http://www.mathematik.uni-kassel.de/~meister/buch_online zum Download bereit.

