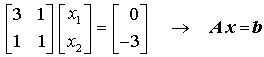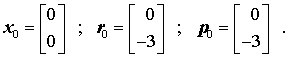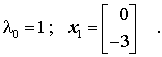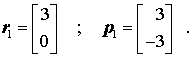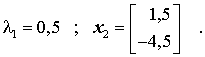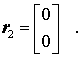Methode der konjugierten Gradienten

Minimalproblem und lineares Gleichungssystem

Die dem Verfahren der konjugierten Gradienten zu Grunde liegende Idee ist dem Ingenieur durch die Energieverfahren der Mechanik vertraut. Dies soll hier an einem kleinen Beispiel in Erinnerung gerufen werden (für den nur am mathematischen Sachverhalt interessierten Leser ist es unerheblich, ob er den Mechanik-Hintergrund der folgenden Ausführungen versteht, er braucht ihn nur zur Kenntnis zu nehmen):

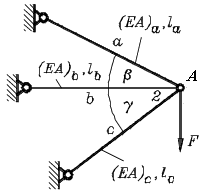Für ein (statisch unbestimmtes) elastisches Tragwerk, wie es nebenstehend abgebildet ist (wird im Kapitel "Der Stab als finites Element" behandelt), kann die Verformungsberechnung mit Hilfe des "Prinzips vom Minimum des elastischen Potenzials" durchgeführt werden (siehe z. B. Kapitel "Prinzipien der Mechanik" oder Internet-Site "Grundgleichungen der Finite-Elemente-Methode"): "Die Differenz zwischen der im System gespeicherten Formänderungsenergie und der so genannten "Endwertarbeit" der äußeren Kräfte ist für den sich tatsächlich einstellenden Verformungszustand ein Minimum".

Für das skizzierte Tragwerk wird der Verformungszustand durch die Horizontalverschiebung u_x und die Vertikalverschiebung u_y des belasteten Knotens A beschrieben (die Lagerung der anderen Knoten lässt keine weiteren Verformungen zu). Mit der Formel für die Formänderungsenergie für den geraden Stab, die man z. B. im Kapitel "Formänderungsenergie" findet, liefert das Prinzip vom Minimum des elastischen Potenzials (mit der Annahme eines linear veränderlichen Verschiebungsverlaufs in Längsrichtung der einzelnen Stäbe):

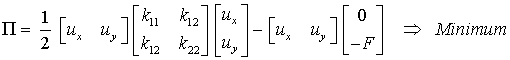
bzw.

mit der (symmetrischen und positiv definiten) Steifigkeitsmatrix K. Die Herleitung der Elemente k_{i i} dieser Matrix für den oben skizzierten allgemeinen Fall findet man im Kapitel "Der Stab als finites Element". Hier sollen zur Vereinfachung die speziellen Zahlenwerte

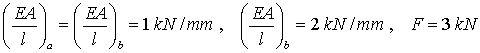
angenommen werden. Dann kann die Bedingung so formuliert werden: Die sich tatsächlich einstellenden Knotenverschiebungen u_x und u_y des Lastangriffspunktes minimieren den folgenden Ausdruck:

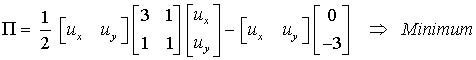
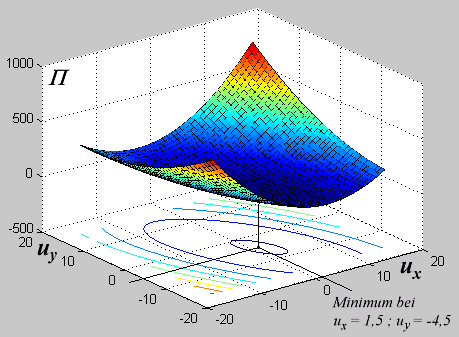(die Dimensionen der Zahlenwerte wurden weggelassen, die Verschiebungen ergeben sich mit der Dimension mm). Nebenstehend ist die Funktion Π(u_x,u_y) dargestellt, die gesuchte Lösung ist in der  u_x-u_y-Ebene, in der die Höhenlinen der Funktion gezeichnet wurden, zu finden.

Natürlich lässt sich das Ergebnis auch analytisch finden. Die von den beiden Variablen u_x und u_y abhängige Funktion Π hat genau dort einen Extremwert (Minimum), wo die beiden partiellen Ableitungen nach diesen Variablen verschwinden. Nach den Regeln für die Ableitungen von Matrixausdrücken folgt aus der Bedingung

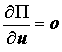
ein lineares Gleichungssystem mit der entsprechenden Lösung:

 

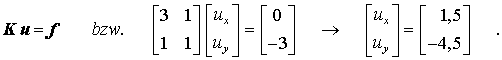
Methode der konjugierten Gradienten

Zur Lösung des linearen Gleichungssystems mit n Unbekannten

mit der symmetrischen und positiven Koeffizientenmatrix A wird nun genau der entgegengesetzte Weg zu dem oben beschrieben Verfahren gewählt: Es wird das zu dem Gleichungssystem analoge Minimalproblem

betrachtet, wobei der Vektor x gesucht wird, für den F minimal wird. Die Strategie ist, dass man mit einem Startvektor x₀ beginnt und eine Folge von iterierten Vektoren x₁, x₂, x₃, ... mit dem Ziel erzeugt, dass diese sich immer mehr dem Lösungsvektor nähern, der F zum Minimum macht.  Dies hat sich zu einem umfangreichen Spezialgebiet der numerischen Mathematik entwickelt, auf das hier nicht eingegangen werden soll. Die Stichworte dazu, für die man auch im Internet zahlreiche Seiten findet, lauten u. a.: "Krylow-Unterraum-Verfahren", "Methode des steilsten Abstiegs" und "Verfahren der konjugierten Richtungen". Hier soll ausschließlich die "Methode der konjugierten Gradienten" betrachtet werden, die eine gewisse Sonderstellung unter den Verfahren dieser Klasse einnimmt.

Bei der "Methode der konjugierten Gradienten" nähert man sich dem Minimum von F, indem man auf der Fläche F(x), beginnend an einem beliebigen Startpunkt jeweils in die Richtung "wandert", dass man sich dem Minimum auf optimale Weise nähert, wobei das Wort "optimal" für jeden Schritt so zu verstehen ist, dass man aus den zu diesem Zeitpunkt verfügbaren Informationen eine Richtung wählt, die theoretisch garantiert, dass nach n Schritten der Minimalpunkt (und damit die Lösung des Gleichungssystems) erreicht wird.

Gleichungssystem: Anfangswerte: Iterationsschritt  i = 0: Vorbereitung des Iterationsschrittes i = 1: Iterationsschritt  i = 1: Vorbereitung des Iterationsschrittes i = 2: Residuenvektor = Nullvektor, Prozess beendet.

In Kurzfassung kann die Methode der konjugierten Gradienten wie folgt formuliert werden, rechts daneben findet man jeweils die Rechnung für das Gleichungssystem, das oben für das Stabwerk formuliert wurde:

• Gestartet wird mit einem beliebigen Vektor x₀ (dies kann auch ein Nullvektor sein), mit dem ein erster "Residuenvektor" r₀ berechnet wird, der auch als erster "Korrekturvektor" p₀ verwendet wird:

• Jeder Iterationsschritt i folgt folgender Strategie: Der Vektor x_i+1 wird durch Korrektur des Vektors x_i in die Richtung p_i berechnet, wobei die "Schrittlänge des p_i-Schrittes" durch einen Faktor λ_i bestimmt wird:

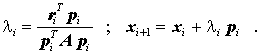
• Als Vorbereitung des folgenden Iterationsschrittes werden ein neuer Residuenvektor r_i+1 und ein neuer Korrekturvektor p_i+1 berechnet:

              

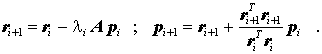
• Es folgt der nächste Integrationsschritt nach den oben angegebenen Formeln. Der Prozess konvergiert, wenn Rundungsfehler keine Rolle spielen, nach n Iterationsschritten (i = 0, 1, 2, ... , n-1). Die Methode der konjugierten Gradienten kann also sowohl als Iterationsverfahren als auch als direktes Verfahren gesehen werden, das wie die Eliminationsverfahren das Ergebnis nach einer endlichen Anzahl von Operationen liefert.

Man beachte die typische Besonderheit der iterativen Verfahren: Die Koeffizientenmatrix A wird ausschließlich für die Operation "Matrix · Vektor" verwendet (die Bildung des Produkts Ap_i muss natürlich in jedem Iterationsschritt einschließlich der Vorbereitung des folgenden Schrittes nur einmal ausgeführt werden). Die Matrix A selbst wird nicht verändert (das für die Eliminationsverfahren typische Problem des "Fill-in" gibt es bei Iterationsverfahren nicht). Deshalb können die Vorteile dünn besetzter Matrizen voll genutzt werden.

Andererseits sind die iterativen Verfahren nicht so stabil wie die direkten Verfahren. Man vergleiche hierzu die beiden Seiten "Testrechnungen mit iterativen Verfahren (1)" und "Testrechnungen mit iterativen Verfahren (2)". Eine Verbesserung kann durch "Präkonditionierung" erreicht werden, das oben vorgestellte Verfahren kann z. B. sehr einfach modifiziert werden zum "Präkonditionierten Konjugierte-Gradienten-Verfahren".