Ausgleichsrechnung
Immer dann, wenn eine mathematische Funktion aus vorgegebenen Punkten bestimmt werden soll, sind mindestens so viele Punkte erforderlich, wie Freiwerte in der Funktion festzulegen sind (Beispiel: Eine Gerade ist durch zwei Punkte eindeutig bestimmt).
Wenn mehr Punkte als erforderlich bekannt sind (z. B. eine größere Messreihe), kann man im Allgemeinen nicht erwarten, dass die Funktion durch alle Punkte verläuft (wenn z. B. 5 Messpunkte für die Bestimmung einer Geraden verfügbar sind, wäre es eher zufällig, wenn alle tatsächlich auf einer Geraden liegen). In diesen Fällen gilt es, die "beste Funktion" zu ermitteln, die sich den vorgegebenen Punkten in einem bestimmten Sinn möglichst gut annähert. Nach einem Vorschlag von Gauß hat sich in der so genannten "Ausgleichsrechnung" das Prinzip durchgesetzt, die "Summe der Quadrate der Abweichungen" zu minimieren.
Kugelstoßen: Für die Bestimmung der Flugbahn der Kugel steht aus Videoaufnahmen folgende Messreihe zur Verfügung:
|
Bei Vernachlässigung des Luftwiderstands darf angenommen werden, dass die Kugel sich auf einer quadratischen Parabel bewegt, die durch folgende Gleichung beschrieben werden kann:
y = a0 + a1x + a2x2 .
Wenn nur drei Punkte verfügbar wären, dann könnten die drei Parameter a0, a1 und a2 eindeutig bestimmt werden. Hier soll die Parabel bestimmt werden, die sich den sechs Punkte im oben genannten Sinn am besten annähert. Einsetzen der Punktkoordinaten in die Parabelgleichung führt auf folgende 6 Gleichungen:
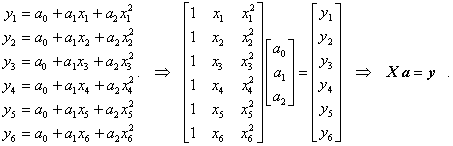
Es ist ein Gleichungssystem mit 6 Gleichungen für die Bestimmung der 3 Unbekannten a0, a1 und a2. Die Lösung kann im Allgemeinen nicht alle 6 Gleichungen erfüllen, in jeder Gleichung wird sich eine Abweichung
ergeben. Die Lösung des überbestimmten Gleichungssystems wird nun so bestimmt, dass die Summe der Quadrate dieser Abweichungen minimal wird:
Als Minimalbedingungen werden die partiellen Ableitungen nach a0, a1 und a2 gleich Null gesetzt:
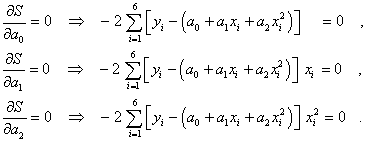
Diese so genannten "Normalgleichungen" für die Bestimmung von a0, a1 und a2 bilden folgendes Gleichungssystem:
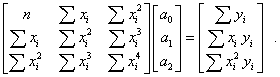
Das Gleichungssystem hat eine symmetrische (positiv definite) Koeffizientenmatrix. Die Grenzen an den Summenzeichen wurden absichtlich weggelassen, um anzudeuten, dass diese Gleichungen für eine beliebige Zahl von Stützpunkten n gelten (im betrachteten Beispiel ist n = 6).
|
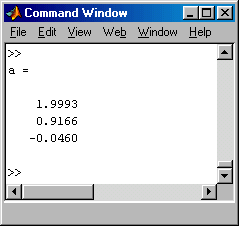
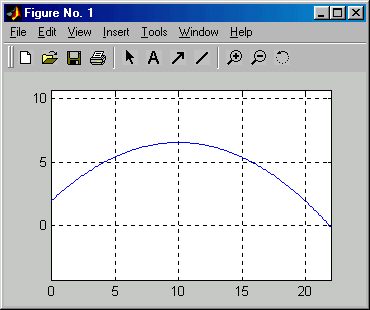
Das nachstehend zu sehende Matlab-Script realisiert diese Rechnung für das betrachtete Beispiel. In das nebenstehend zu sehende Command Window werden die drei Werte a0, a1 und a2 ausgegeben, die die Ausgleichsparabel definieren, in ein Graphik-Window (darunter zu sehen) wird die Parabel gezeichnet: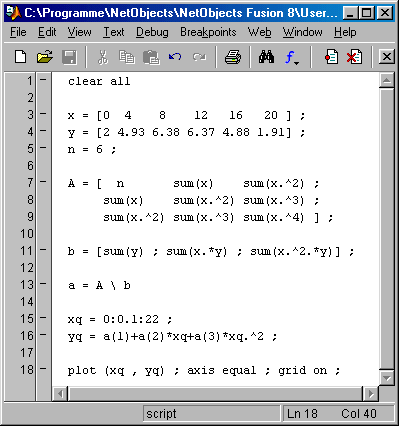 
|
|
Interaktive Lösung überbestimmter Gleichungssysteme
Mit dem Programm "Überbestimmtes lineares Gleichungssystem" unter TM-interaktiv.de kann man das oben angegebene Gleichungssystem mit 6 Gleichungen und 3 Unbekannten direkt lösen. Das hier behandelte Problem wird dort als eines von mehreren Anwendungsbeispielen ausführlich beschrieben.
Lösung überbestimmter Gleichungssysteme in Matlab
Der oben am Beispiel beschriebene Weg zur Lösung eines überbestimmten Gleichungssystems über die Normalgleichungen ist in Matlab direkt implementiert, so dass man Matlab das überbestimmte Gleichungssystem direkt anbieten kann.
Wenn man den Backslash-Operator, mit dem in Matlab ein lineares Gleichungssystem A x = b gelöst werden kann, mit einer Matrix A verwendet, deren Zeilenanzahl größer als die Spaltenanzahl ist, dann wird automatisch das überbestimmte Gleichungssystem nach den Regeln der Ausgleichsrechnung gelöst.
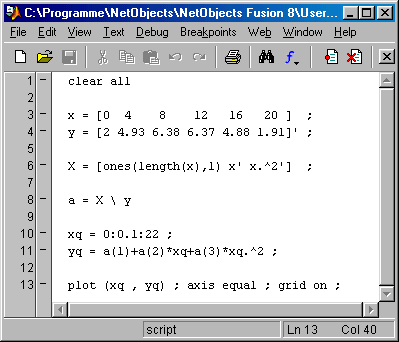
Das nebenstehend zu sehende Matlab-Script demonstriert dies. Es wird direkt das oben angegebene überbestimmte Gleichungssystem
X a = y
(Matrix X hat 6 Zeilen und 3 Spalten) aufgebaut und gelöst. Die Ergebnisse sind mit den oben angegebenen Ergebnissen identisch.
Hinweis: Die Fähigkeit des Backslash-Operators in Matlab, auch überbestimmte Gleichungssysteme lösen zu können, kann auch sehr effektiv für die Kontrolle des aufgestellten Gleichungssystems genutzt werden. An einem Statik-Problem (Klicken auf das kleine Bild rechts) wird dies demonstriert. Auf diese Weise werden sogar die verwendeten Gleichgewichtsbedingungen einer Kontrolle unterzogen.
Zum Download verfügbar sind die abgebildeten Matlab-Scripts Ausgleichsparabel1.m und Ausgleichsparabel2.m.
