 Das Beispiel
Das Beispiel
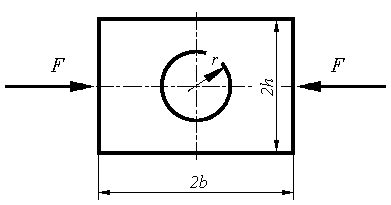
Als Beispiel soll das Gleichungssystem dienen, das aus dem Finite-Elemente-Modell der nebenstehend zu sehenden ebenen Rechteckscheibe mit kreisförmigem Loch entsteht. Dieses Beispiel wird hier ausführlich beschrieben. Es ist geradezu ein Klassiker für die Einführung in die Finite-Elemente-Methode, weil damit mit überschaubarem Aufwand eine praktisch wichtige Aufgabe gelöst wird, die sich der analytischen Lösung entzieht.
Wegen der doppelten Symmetrie wird nur ein Viertel der Scheibe vernetzt, und die Punkte auf den Symmetrielinienn werden so gelagert, dass sie sich nur entlang dieser Linien bewegen können.
Das entstehende lineare Gleichungssystem hat beste Voraussetzungen für erfolgreiche Lösungsversuche: Die Koeffizientenmatrix ist symmetrisch, positiv definit und von sehr guter Kondition.
 Die Lösungsverfahren
Die Lösungsverfahren
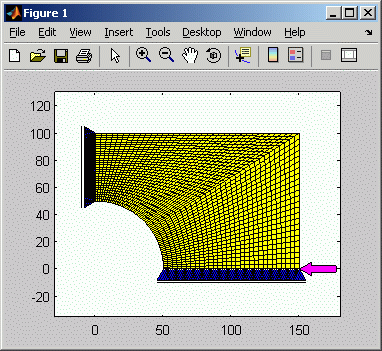
Das lineare Gleichungssystem wird für unterschiedlich feine Vernetzung erzeugt (rechts sieht man ein vernetztes Scheibenviertel mit 1800 Elementen), die Koeffizientenmatrix wird als "Sparse matrix" gespeichert. Das Gleichungssystem wird mit folgenden von Matlab bereitgestellten Verfahren gelöst:
- Der "Standard-Solver Backslash" arbeitet mit direkten Verfahren. Er analysiert die Eigenschaften des übergebenen Systems und entscheidet sich danach für ein geeignetes Verfahren. Für das hier behandelte Beispiel wird es das Cholesky-Verfahren mit vorab ausgeführter Fill-in-Optimierung sein.
- Von den 9 in Matlab angebotenen iterativen Verfahren wird hier die Function pcg ("preconditioned conjugate gradient") gewählt, weil dieses Verfahren zu den Eigenschaften der Koeffizientenmatrix passt. Die Standardeinstellungen der iterativen Verfahren in Matlab sind so, dass sie für Aufgaben dieser Art zum Misserfolg führen. Deshalb werden
- die Anzahl der erlaubten Iterationsschritte deutlich erhöht,
- die Toleranz für die erlaubte Abweichung der Norm des Restvektors (Abbruchschranke) unter Inkaufnahme ungenauerer Ergebnisse vergrößert (von 10-6 auf 10-2),
- mit dem "Incomplete Cholesky"-Verfahren ein Präkonditionierer berechnet und an pcg übergeben, von dem erwartet werden darf, dass er die Konvergenz des Verfahrens deutlich beschleunigt.
Das Matlab-Script und die Testrechnungen
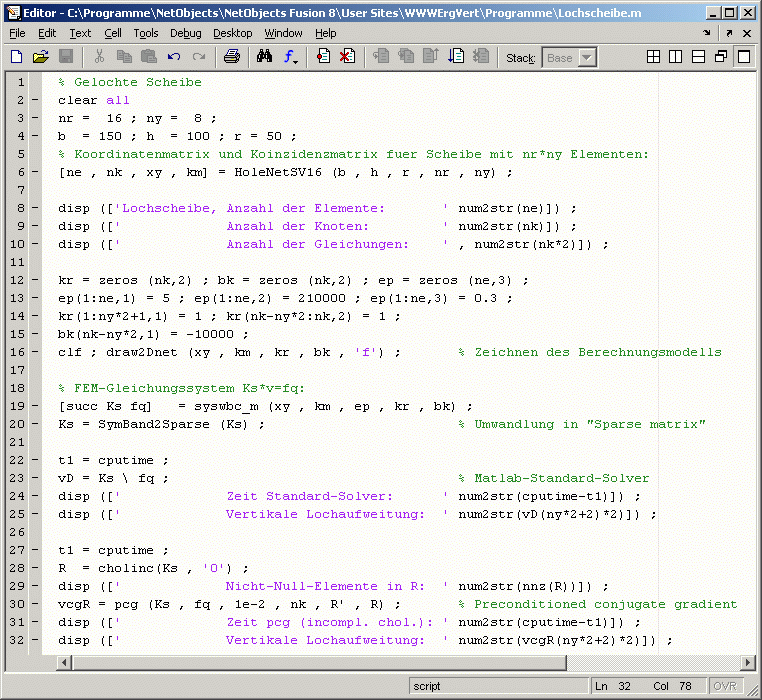
Im nachfolgend zu sehenden Script wird das Gleichungssystem in den Zeilen 3 bis 20 erzeugt. Dies ist für die hier anzustellenden Betrachtungen nicht interessant (für Interessenten: Matlab-Femset). In Zeile 3 wird allerdings mit den beiden Paramtern nr und ny die Feinheit des FEM-Netzes und damit die Anzahl der Unbekannten für das lineare Gleichungssystem festgelegt.
In Zeile 23 wird das Gleichungssystem mit dem Matlab-Standard-Solver (direktes Verfahren), in Zeile 30 mit dem Konjugierte-Gradienten-Verfahren gelöst. Als Referenzwert (für die Kontrolle der Genauigkeit der Rechnung) wird die vertikale Aufweitung des Kreisausschnitts infolge der Belastung gewählt (Ausgabe in den Zeilen 25 bzw. 32).
- Die Lösungen mit dem Matlab-Standard-Solver (direktes Verfahren) waren sämtlich problemlos, die erforderlichen Rechenzeiten bemerkenswert gering..
- Die Lösungen mit dem Konjugierte-Gradienten-Verfahren verlangen einige Versuche, bis die richtige Einstellung für den Präkonditionierer gefunden ist:
- Die Standardvariante für das "Incomplete Cholesky"-Verfahren ist (wie oben in Zeile 28 zu sehen) der Aufruf mit dem String '0' als zweitem Parameter. In diesem Fall werden nur genau die Elemente der Dreicksmatrix erzeugt, deren Positionen auch in der Matrix Ks Nicht-Null-Elemente erhalten. Diese "klassische" Variante war nur für kleine Gleichungssysteme (mit weniger als 1000 Gleichungen) möglich, bei größeren Systemen kam die folgende Fehlermeldung:

- Matlab bietet noch eine andere Aufrufvariante für cholinc an: Als zweiter Parameter kann eine so genannte "Drop tolerance" angegeben werden, mit der der Füllungsgrad der erzeugten Dreiecksmatrix beliebig gesteuert werden kann (es können deutlich weniger Elemente als bei der klassischen Variante sein, andererseits auch deutlich mehr). In den beiden Extremfällen erhält man eine reine Diagonalmatrix (Drop tolerance 1) bzw. das Ergebnis der kompletten Cholesky-Zerlegung (Drop tolerance 0). Die folgende Tabelle zeigt das Ergebnis einer Testserie mit unterschiedlichen Werten für die Drop tolerance (durchgeführt mit einem Gleichungssystem mit 19682 Gleichungen):
|
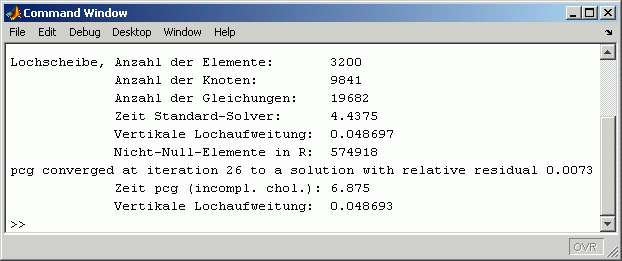 Rechts sieht man im Command Window die Ergebnisse der Berechnung mit der Drop tolerance 0,001, für die sich eine Rechtsdreiecksmatrix mit 574 918 Elementen ergibt. Zum Vergleich: Die komplette Cholesky-Zerlegung ergibt eine Dreiecksmatrix mit 4 022 393 Elementen, die "klassische Variante" des "Incomplete Cholesky" führt auf eine Dreiecksmatrix mit 309 733 Elementen.
Rechts sieht man im Command Window die Ergebnisse der Berechnung mit der Drop tolerance 0,001, für die sich eine Rechtsdreiecksmatrix mit 574 918 Elementen ergibt. Zum Vergleich: Die komplette Cholesky-Zerlegung ergibt eine Dreiecksmatrix mit 4 022 393 Elementen, die "klassische Variante" des "Incomplete Cholesky" führt auf eine Dreiecksmatrix mit 309 733 Elementen.
Man erkennt in der Tabelle, dass mit einem höheren Füllungsgrad der Dreiecksmatrix, die als Präkonditionierer verwendet wird, das anschließende Iterationsverfahren immer schneller konvergiert. Allerdings erfordert die Herstellung besserer Präkonditionierer auch einen höheren Aufwand. Ein gewisses Optimum ergibt sich bei einer Drop tolerance von 0,001, deshalb werden die folgenden Berechnungen mit unterschiedlich großen Gleichungssystemen mit Präkonditionierern durchgeführt, die mit dieser Drop tolerance erzeugt werden.
Vergleich der Rechenzeiten für Gleichungssysteme unterschiedlicher Größe:
|
Fazit
- Die Lösung des linearen Gleichungssystems mit dem Matlab-Standard-Solver, der mit direkten Verfahren arbeitet, war völlig problemlos.
- Die Lösung des Gleichungssystems mit dem Konjugierte-Gradienten-Verfahren verlangte einige Voruntersuchungen, die sich in folgenden Aussagen zusammenfassen lassen:
- Lösungsversuche ohne Präkonditionierung sind überhaupt nicht zu empfehlen.
- Die Skalierung als Verfahren für die Präkonditionierung führt zu einer Verbesserung, aber bei größeren Systemen ergeben sich auch damit inakzeptable Rechenzeiten.
- Das "Incomplete Cholesky"-Verfahren zur Erzeugung eines Präkonditionierers in der "klassischen Variante" (es werden genau die Elemente bei der Dreieckszerlegung erzeugt, deren Positionen in der Ausgangsmatrix auch mit Nicht-Null-Elementen besetzt waren) versagt leider häufig bei größeren Matrizen (siehe auch "Test: Präkonditionierung mit Incomplete Cholesky").
- Die von Matlab angebotene Variante des "Incomplete Cholesky", ein beliebiges Fill-in über die Drop tolerance zuzulassen, führt schließlich zu sehr effektiven Präkonditionierern, wenn man eine geeignete Drop tolerance benutzt (gegebenenfalls durch Versuche zu ermitteln).
- Dass die Rechenzeiten trotz der mühsamen Vorarbeit zum Finden eines möglichst optimalen Präkonditionierers für das Iterationsverfahren trotzdem höher waren, kann durchaus auch daran liegen, dass dieses in Matlab nicht so effektiv programmiert ist wie der Matlab-Standard-Solver.
Zum Download verfügbar sind
- das oben abgebildete Matlab-Script als Lochscheibe.m,
- die aus dem Matlab-Script aufgerufenen Functions HoleNetSV16.m und draw2Dnet.m und die DLL syswbc_m.dll.

