Problem
Untersucht werden soll ein lineares Gleichungssystem mit mehr Gleichungen als Unbekannten, das in folgender Form vorliegt (gegeben sind die Koeffizienten aij auf der linken Seite und die bi auf der rechten Seite, gesucht sind die Unbekannten xj):
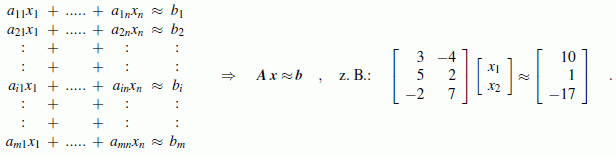
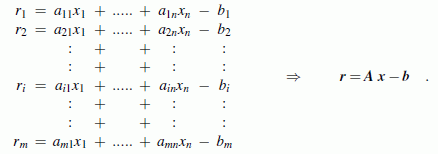
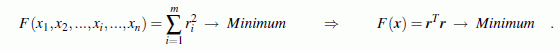
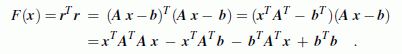
Gaußsche Normalgleichungen:
Für ein überbestimmtes lineares Gleichungssystem mit einer Koeffizientenmatrix A mit m Zeilen und n Spalten (m ≥ n) findet man die Gaußschen Normalgleichungen durch Linksmultiplikation auf beiden Seiten mit der transponierten Koeffizientenmatrix:
| Überbestimmtes Gleichungssystem | Gaußsche Normalgleichungen | |
| A x ≈ b | → | AT A x = AT b |
Dieses Gleichungssystem hat eine symmetrische Koeffizientenmatrix. Seine Lösung ist die Näherungslösung für das Ausgangssystem im Sinne der Forderung nach dem Minimum der Fehlerquadratsumme.
Beispiel
Für das folgende Gleichungssystem mit 3 Gleichungen und 2 Unbekannten sollen die Gaußschen Normalgleichungen aufgeschrieben und gelöst werden:
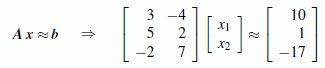
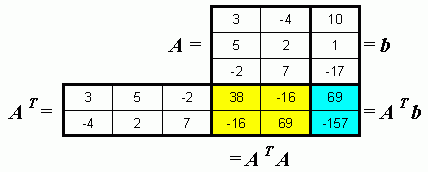 Nebenstehend sieht man das
Falksche Schema
Beispiel für Matrixmultiplikation
Nebenstehend sieht man das
Falksche Schema
Beispiel für Matrixmultiplikation
 ,
mit dem die Koeffizientenmatrix
ATA
und die rechte Seite
ATb
für die Normalgleichungen berechnet werden.
Das kleine Gleichungssystem
,
mit dem die Koeffizientenmatrix
ATA
und die rechte Seite
ATb
für die Normalgleichungen berechnet werden.
Das kleine Gleichungssystem
erfüllt keine der drei Gleichungen des überbestimmten Systems exakt, aber alle Gleichungen "bestmöglich". Zu dem Ergebnis kann man allerdings viel einfacher kommen, wenn man das nachfolgend beschriebene Angebot nutzt.
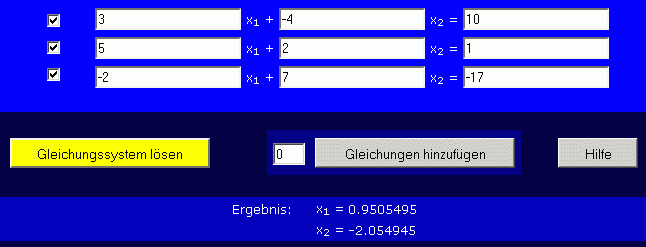
Programm "Überbestimmtes lineares Gleichungssystem" unter TM-interaktiv.de
Das Programm "Überbestimmtes lineares Gleichungssystem" unter TM-interaktiv.de realisiert die Berechnung exakt nach dem oben beschriebenen Algorithmus. Dem Programm kann das überbestimmte Gleichungssystem direkt eingegeben werden, für das gerade behandelte kleine Beispiel sehen Eingabe und Ergebnis so aus: