Beispiele zur Matrizenmultiplikation

Matrixmultiplikation

Die Definition des Produkts der beiden Matrizen A und B

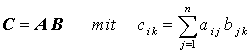
lässt sich besonders anschaulich im so genannten Falkschen Schema darstellen, wie es das folgende Beispiel zeigt:

Man entnimmt diesem Schema alle wichtigen Aussagen über das Matrizenprodukt:

• Jedes Element der Ergebnismatrix C entsteht aus einem Skalarprodukt Das Skalarprodukt
  
  
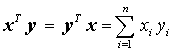
  ist für Vektoren gleicher Dimension definiert, z. B.:
  
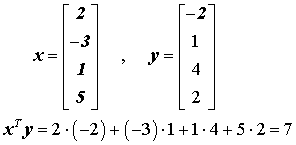  einer Zeile von A mit einer Spalte von B, wie es farblich für das Element v₃₂ gekennzeichnet ist.
• Damit wird auch klar, dass die Spaltenanzahl von A mit der Zeilenanzahl von B übereinstimmen muss (nur in der Reihenfolge AB sind diese beiden Matrizen "verkettbar").
• Die Zeilenanzahl der Ergebnismatrix entspricht der Zeilenanzahl des ersten Faktors, die Spaltenanzahl der Spaltenanzahl des zweiten Faktors.

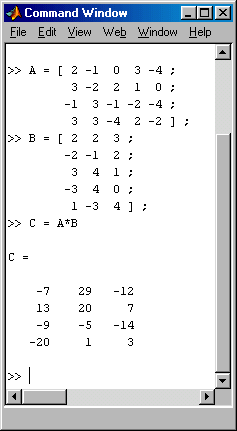
In Matlab kann die Matrixmultiplikation direkt in der üblichen Schreibweise programmiert werden. Der nebenstehend zu sehende Bildschirm-Schnappschuss zeigt das Command Window, in dem zunächst die beiden Matrizen A und B definiert werden (Elemente werden durch Leerzeichen oder Komma getrennt, der Übergang zu einer neuen Zeile wird durch das Semikolon signalisiert).

Schließlich wird mit der Operation C=A*B das Produkt berechnet und angezeigt (entsprechend der Matlab-Regel, dass Anweisungen, die nicht mit Semikolon abgeschlossen werden, ihr Ergebnis ins Command Window schreiben).

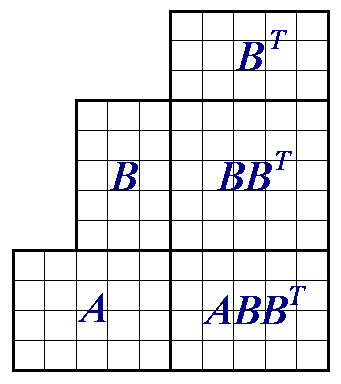
Das Falksche Schema eignet sich für Matrixprodukte mit beliebig vielen Faktoren (heute natürlich nur noch zur Veranschaulichung, die Rechnungen überträgt man natürlich einer geeigneten Software). Am Beispiel der Bildung des Produkts

A B B^T

mit den bereits oben verwendeten Matrizen wird dies für ein Produkt mit drei Matrizen demonstriert:

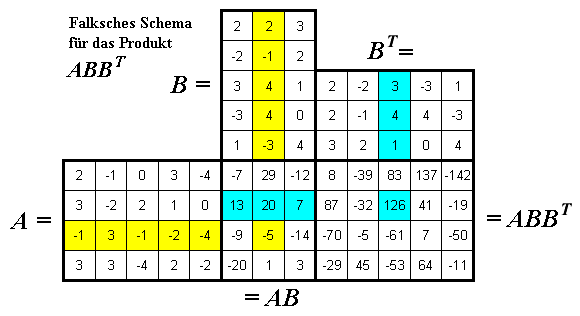
In diesem Schema wird zunächst das Produkt AB berechnet, um danach das Ergebnis mit B^T zu multiplizieren. Wie für das erste Produkt ist auch für das zweite Produkt ein Skalarprodukt Das Skalarprodukt


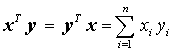
ist für Vektoren gleicher Dimension definiert, z. B.:

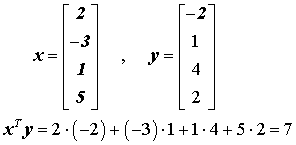zur Erzeugung eines einzelnen Elements farblich hervorgehoben.

Weil das Produkt mehrerer Matrizen assoziativ ist, kann man auch zunächst das Produkt BB^T bilden, um dieses dann von links mit A zu multiplizieren. Nachfolgend ist rechts das dafür zu verwendende Falksche Schema angedeutet. Man verifiziert leicht, dass der erforderliche Aufwand stark von der Wahl der Reihenfolge der Multiplikationen abhängig sein kann. In diesem Fall sind für die Realisierung des oben ausgefüllten Schemas 120 Multiplikationen erforderlich, bei Verwendung des nachfolgemden Schemas würde man 175 Multiplikationen ausführen müssen. Bei großen Matrizen kann man auch bei der Verwendung des Computers die Rechenzeiten durch die Reihenfolge der Operationen nicht unwesentlich beeinflussen.

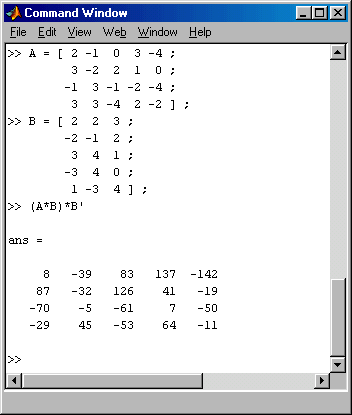
Nachfolgend ist links die Realisierung dieser Berechnung im Command Window von Matlab zu sehen:

Die transponierte Matrix wird in Matlab mit Apostroph dargestellt. Die (eigentlich überflüssigen) Klammern erzwingen, dass tatsächlich als erste Multiplikation AB ausgeführt wird.

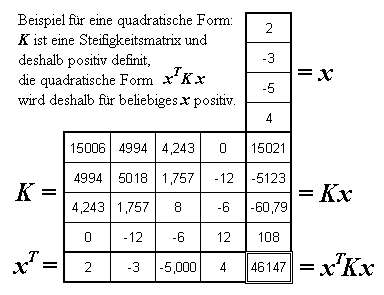Das nebenstehende Beispiel zeigt die Berechnung einer so genannten quadratischen Form

die als Ergebnis eine skalare Größe ergibt (das Falksche Schema macht dies deutlich). Für so genannte positiv definite Matrizen ist das Ergebnis für jeden beliebigen Vektor x immer positiv, was hier an einem Beispiel gezeigt wird.