Einen nicht verschwindenden Vektor x (x ist also kein Nullvektor), der der Gleichung
genügt, nennt man Eigenvektor der quadratischen Matrix A, den zugehörigen Wert λ Eigenwert. In der Technischen Mechanik findet man Eigenwerte z. B. als Eigenfreuenzen eines Schwingungssystems (vgl. z. B. "Eigenschwingungen mit der Finite-Elemente-Methode", "Biegeschwingungen gerader Träger" oder diese Aufgabe), die u. a mit der Finite-Elemente-Methode oder dem Differenzenverfahren auf ein Matrizeneigenwertproblem führt). Auch die kritischen Lasten bei Stabilitätsproblemen werden vornehmlich über die Eigenwerte von Matrizen bestimmt (vgl. z. B. "Knickstab unter Eigengewicht" oder "Verfahren von Ritz für Knickstäbe").
Die Eigenwerte einer Matrix sind gegenüber Ähnlichkeitstransformationen invariant, während sich die Eigenvektoren entsprechend dem Übergang zur neuen Basis transformieren.
Auch die Eigenwerte von reellen Matrizen
können komplex sein. Deshalb ist ein Sonderfall besonders wichtig:
Eine (reelle)
symmetrische n-dimensionale Matrix
Symmetrische Matrix:
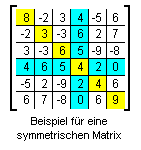Die Elemente einer symmetrischen Matrix sind zur Hauptdiagonalen
(im Beispiel gelb unterlegt) spiegelbildlich gleich.
Das bedeutet auch, dass die Elemente einer Zeile gleich sind mit den
Elementen der entsprechenden Spalte (hier für die 4. Zeile bzw. Spalte
farblich gekennzeichnet).
besitzt n verschiedene Eigenvektoren (die zugehörigen Eigenwerte brauchen nicht alle verschieden voneinander zu sein). Die Eigenwerte solcher Matrizen sind sämtlich reell, die Eigenvektoren bilden ein Orthogonalsystem.
Die Matrizeneigenwertprobleme sind ein umfangreiches Spezialgebiet der Matrizen-Numerik.
Zu jeder
symmetrischen Matrix
Symmetrische Matrix:
Die Elemente einer symmetrischen Matrix sind zur Hauptdiagonalen
(im Beispiel gelb unterlegt) spiegelbildlich gleich.
Das bedeutet auch, dass die Elemente einer Zeile gleich sind mit den
Elementen der entsprechenden Spalte (hier für die 4. Zeile bzw. Spalte
farblich gekennzeichnet).
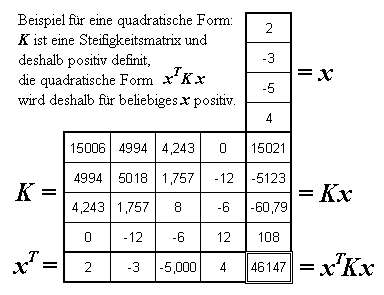
A gehört eine so genannte quadratische Form
Ausdrücke dieser Art finden sich in der Technischen Mechanik z. B. als kinetische Energie eines Massensystems oder als Formänderungsarbeit eines elastostatischen Systems. Unter der (für die genannten Beispiele stets erfüllten) Bedingung
wird die Matrix A positiv definit genannt. Solche Matrizen sind auch regulär.
Bestimmte Verfahren der Matrizen-Numerik (z. B. die Cholesky-Zerlegung einer symmetrischen Matrix) setzen die positive Definitheit voraus. Dies ist eigentlich eine Einschränkung der Verwendbarkeit dieser Verfahren, wird aber z. B. in der Technischen Mechanik mit Vorteil genutzt: Weil die Matrizen für die meisten Mechanik-Probleme (siehe oben genannte Beispiele) positiv definit sein müssen, ist der "Absturz" der Rechnung mit solchen Verfahren ein sicheres Indiz dafür, dass die Matrix falsch ist.
