Anfangswertprobleme

Bei einer gewöhnlichen Differenzialgleichung n-ter Ordnung
enthält die allgemeine Lösung n Integrationskonstanten. Es können n zusätzliche Bedingungen formuliert werden, mit denen diese Integrationskonstanten zu bestimmen sind, so dass sich die spezielle Lösung des durch Differenzialgleichung und Zusatzbedingungen beschriebenen Problems ergibt.
Wenn alle Zusatzbedingungen für die gleichen Stelle x0 gegeben sind (der Funktionswert y und die Ableitungen bis zur (n−1)-ten Ordnung sind an dieser Stelle vorgeschrieben), dann spricht man von einem Anfangswertproblem (im Gegensatz zum Randwertproblem, bei dem diese Bedingungen für unterschiedliche x-Werte gegeben sind).
Praxisnahe Rand- und Anfangswertaufgaben sind nur in seltenen Ausnahmefällen geschlossen lösbar. Während für lineare Differenzialgleichungen leistungsfähige Lösungsstrategien und numerische Verfahren (z. B. das Differenzenverfahren) verfügbar sind, beschränken sich die Lösungsmöglichkeiten bei nichtlinearen Differenzialgleichungen weitgehend auf Anfangswertprobleme.
Glücklicherweise sind die im Regelfall nur mit nichtlinearen Bewegungs-Differenzialgleichungen zu beschreibenden Probleme der Technischen Mechanik fast immer Anfangswertprobleme: Die unabhängige Variable ist die Zeit t, und in den Differenzialgleichungen tauchen die Bewegungskoordinaten und deren 1. und 2. Ableitungen nach t auf (Geschwindigkeiten bzw. Beschleunigungen). Die Anfangsbedingungen werden als Aussagen über die Lage (Bewegungskoordinate) und die Anfangsgeschwindigkeit für einen speziellen Zeitpunkt t0 formuliert.

Die nebenstehende Animation zeigt ein besonders einfaches Beispiel. Die Bewegung eines Stabpendels mit großen Ausschlägen wird durch folgendes Anfangswertproblem beschrieben (die Bewegung wird mit dem Winkel φ verfolgt, l ist die Länge des Stabs, g die Erdbeschleunigung):
Bei der Formulierung der Anfangsbedingungen wurde angenommen, dass das Pendel zum Zeitpunkt t = 0 ohne Anfangsgeschwindigkeit aus der Anfangslage φ = φ0 freigelassen wird.
Selbst dieses einfache und idealisierte Problem (Reibungsfreiheit, Vernachlässiging des Luftwiderstands) kann nur numerisch gelöst werden. Hier findet man die Beschreibung der kompletten Lösung.
Die für die numerische Integration von Anfangswertprobleme verfügbaren Lösungsverfahren sind kaum zu überblicken. Dass die leistungsfähigsten Verfahren mit Formelsätzen arbeiten, die (vorsichtig formuliert) etwas unhandlich aussehen, ist unbedeutend, denn eine Handrechnung verbietet sich in der Regel von selbst. Es gibt kaum ein anderes Gebiet, in dem die mathematischen Hilfsmittel mit so viel Vorsicht zu benutzen sind wie bei der numerischen Integration von Anfangswertproblemen (allerdings gibt es auch keine Alternative). Deshalb sollte der Anwender unbedingt die wichtigsten Eigenschaften der verwendeten Verfahren kennen. Hier findet man einen ...
- Überblick über die wichtigsten Verfahren:
Im Skript (PDF, 39 Seiten) "Numerische Integration von Anfangswertproblemen (Teil 1:
Grundlagen)"
Inhalt: Verfahren von Euler-Cauchy, Prädiktor-Korrektor-Verfahren (Heun), Runge-Kutta-Verfahren, Diffenzialgleichungen höherer Ordnung, Differenzialgleichungssysteme, zahlreiche Beispiele, Schrittweitenwahl, Verifizieren der Ergebnisse, Richardson-Extrapolation, Butcher-Arrays, Verfahren von Fehlberg, Verfahren von Dormand-Prince, Ein- und Mehrschrittverfahren, Verfahren von Adams/Bashforth/Moulton, Verfahren von Gear, Verfahrensauswahl findet man die Formelsätze der Verfahren, die in modernen Sofwareprodukten verwendet werden, Informationen über die Lösungsstrategien und die Demonstration an zahlreichen Beispielen.
- Interaktive Lösung von Anfangswertproblemen:
Im Bereich
TM-interaktiv findet man das Angebot
"Anfangswertproblem".
Es wird ein Anfangswertproblem gelöst, das durch ein Differenzialgleichungssystem 1. Ordnung

xi' = fi(t,x1,x2,...) und Anfangsbedingungen
xi(t=t0) = xi0 beschrieben wird (i = 1...n). Typische Anwendungsfälle sind die Bewegungs-Differenzialgleichungen der Kinetik. Dort können Anfangswertprobleme interaktiv (ohne Download einer Software) gelöst werden, was an zahlreichen Beispielen demonstriert wird. - Lösung von Anfangswertproblemen mit Matlab:
Im Skript (PDF, 16 Seiten) ""Numerische Integration von Anfangswertproblemen (Teil 2:
Praxis)"
Inhalt: Systeme mit
mehreren Freiheitsgraden, Kopplung in den Gliedern mit der
höchsten Ableitung, Ereignisse (An- und Abschalten von Antrieben,
Anstoß an Federn, plötzliche Änderung des Bewegungswiderstands, ...),
Realisierung mit Matlab, Matlab ode-Solver, Matlab-Event-Strategie,
Beispiele
werden Lösungsstrategien mit Matlab vorgestellt, an Beispielen erläutert und auf die im Internet verfügbaren Lösungen verwiesen.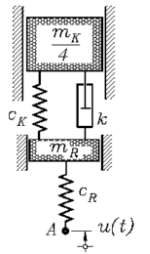
- Beispiele im Internet: Über die folgenden Links kommt man zu Verteilern zu Aufgaben mit Lösungen für Systeme mit einem Freiheitsgrad bzw. Systeme mit mehreren Freiheitsgraden.

