Gewöhnliche Differenzialgleichungen
Eine Differenzialgleichung ist eine Gleichung, in der Differenzialquotienten einer Funktion (oder mehrerer Funktionen) auftreten. Gesucht sind die Funktionen, die diese Gleichung (und gegebenenfalls mehrere Zusatzbedingungen) erfüllen. Gewöhnliche Differenzialgleichungen enthalten ausschließlich gesuchte Funktionen, die nur von einer unabhängigen Variablen abhängig sind (und damit gibt es auch nur Ableitungen nach dieser Variablen). Die höchste in der Differenzialgleichung auftretende Ableitung der gesuchten Funktion bestimmt die Ordnung der Differenzialgleichung.
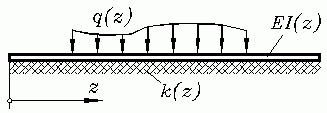
Beispiel: Die Differenzialgleichung des elastisch gebetteten Trägers
Lineare und nichtlineare Differenzialgleichungen
Eine "Lineare Differenzialgleichung" enthält die gesuchte Funktion und deren Ableitungen nur in der ersten Potenz. Es dürfen keine Produkte von gesuchter Funktion und ihren Ableitungen auftreten. Die gesuchte Funktion darf auch nicht in Argumenten von Winkelfunktionen, Logarithmen usw. erscheinen. Die allgemeine lineare Differenzialgleichung n-ter Ordnung kann in der Form
Beispiel: Die oben angegebene Differenzialgleichung des elastisch gebetteten Trägers ist eine lineare Differenzialgleichung.
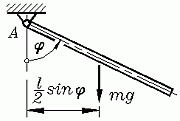
"Nichtlineare Differenzialgleichungen" sind alle Differenzialgleichungen, die nicht nach der oben gegebenen Definition als "linear" klassifiziert werden können.
Beispiel: Die Pendelbewegung eines dünnen Stabs wird durch die nichtlineare Differenzialgleichung
Allgemeine und spezielle Lösungen
Die "Allgemeine Lösung" einer Differenzialgleichung erfüllt die Differenzialgleichung und enthält bei einer Differenzialgleichung n-ter Ordnung n freie "Integrationskonstanten", zu deuten als eine Kurvenschar. Die Integrationskonstanten können durch Zusatzbedingungen (z. B. Randbedingungen, Übergangsbedingungen, Anfangsbedingungen) bestimmt werden, wodurch für diesen speziellen Fall die "Spezielle Lösung" entsteht.
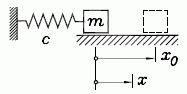
Beispiel: Die reibungsfreie Bewegung einer Masse m, die durch eine Feder (Federzahl c) gefesselt ist, kann durch die lineare Differenzialgleichung zweiter Ordnung
Differenzialgleichungssysteme
Ein "Differenzialgleichungssystem" besteht aus m Differenzialgleichungen, in denen m gesuchte Funktionen enthalten sind.
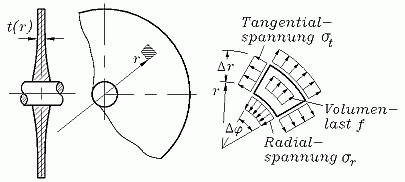
Beispiel 1: Für die Berechnung der Radialspannung σr und der Tangentialspannung σt in einer rotationssymmetrischen Scheibe wird im Kapitel "Rotationssymmetrische Modelle" folgendes Differenzialgleichungssystem hergeleitet:
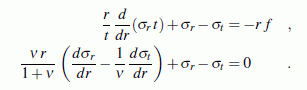
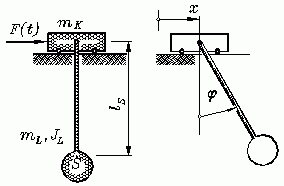
Beispiel 2: Die Bewegung einer Laufkatze mit anhängender Last kann durch die beiden zeitabhängigen Funktionen x(t) und φ(t) beschrieben werden. Die Differenzialgleichungen werden im Kapitel "Prinzipien der Mechanik" hergeleitet:
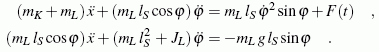
Lösbarkeit
Analytische Lösungen für Differenzialgleichungen oder Differenzialgleichungssysteme zu finden, ist nur in Ausnahmefällen möglich, das heißt: In den meisten Fällen kann man die allgemeine Lösung nicht als Funktion darstellen, die beim Einsetzen die Differenzialgleichungen erfüllen. Für die typischen Differenzialgleichungen der Technischen Mechanik gilt:
- Für eine Differenzialgleichung erster Ordnung gibt es noch relativ gute Chancen für eine analytische Lösung. Geeignete Substitutionen oder die Strategie der "Trennung der Variablen" können zum Erfolg führen. Differenzialgleichungen erster Ordnung sind in der Technischen Mechanik recht selten.
-
Die linearen Differenzialgleichungen
können für einige spezielle Funktionen fi(x) analytisch gelöst werden. Der auch für die Technische Mechanik sehr wichtige Spezialfall der "Linearen Differenzialgleichung mit konstanten Koeffizienten"
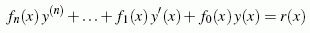 kann für r(x) = 0 (homogene Differenzialgleichung) analytisch gelöst werden. Auch für die in der Technischen Mechanik typischen "rechten Seiten" r(x) findet man Lösungen. Für Systeme linearer Differenzialgleichungen mit konstanten Koeffizienten gelten die gleichen Aussagen.
kann für r(x) = 0 (homogene Differenzialgleichung) analytisch gelöst werden. Auch für die in der Technischen Mechanik typischen "rechten Seiten" r(x) findet man Lösungen. Für Systeme linearer Differenzialgleichungen mit konstanten Koeffizienten gelten die gleichen Aussagen.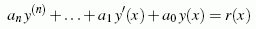
- Nichtlineare Differenzialgleichungen sind nur in seltenen Ausnahmefällen analytisch lösbar. In der Technischen Mechanik sind die Bewegungs-Differenzialgleichungen die typischen Vertreter dieser Art, die (bis auf wenige "akademische Probleme") nur numerisch gelöst werden können.

