Lineare Dgln. mit konstanten Koeffizienten

Allgemeine Form der linearen Differenzialgleichung mit konstanten Koeffizienten

Eine Lineare Differenzialgleichung n-ter Ordnung mit konstanten Koeffizienten

kann unter Verwendung des Summensymbols auch in der Form aufgeschrieben werden.

Grundsätzlich gelten alle Aussagen, die für die linearen Differenzialgleichungen allgemein (ohne die Einschränkung, dass die Koeffizienten konstant sein müssen) gelten. Sie werden hier noch einmal zusammengestellt:

Homogene lineare Differenzialgleichung mit konstanten Koeffizienten

Für die homogene lineare Differenzialgleichung n-ter Ordnung mit konstanten Koeffizienten

gibt es eine zuverlässig funktionierende Strategie, n linear unabhängige Partikulärlösungen (und damit die allgemeine Lösung der homogenen Differenzialgleichung) zu finden. Man wählt den Ansatz (naheliegend, weil sich die e-Funktion bei den Ableitungen reproduziert) mit dem zunächst unbekannten Parameter λ. Mit ergibt sich durch Einsetzen in die Differenzialgleichung: Aus dieser Beziehung hebt sich die Funktion e^x heraus (dieses "Kürzen" ist erlaubt, weil die e-Funktion immer ungleich Null ist) und man erhält mit die so genannte "Charakteristische Gleichung". Diese Gleichung liefert n Lösungen λ₁, λ₂, ... λ_n. Dabei können folgende Fälle auftreten:

• Alle λ_i sind reell und voneinander verschieden: In diesem Fall bilden die Partikulärlösungen
  
  ein Fundamentalsystem (lineare Unabhängigkeit kann mit der Wronskischen Determinante leicht bewiesen werden), und ihre Linearkombination entsprechend
  
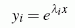  ist die allgemeine Lösung der Differenzialgleichung.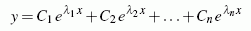
• Die Lösung der charakteristischen Gleichung liefert auch komplexe Lösungen λ_i: Dies ist der typische Fall bei Problemen der Technischen Mechanik. Weil komplexe Nullstellen immer paarweise in der Form
  
  auftreten (zwei zueinander konjugiert komplexe Werte), können die beiden zugehörigen Partikulärlösungen mit Hilfe der Euler-Relation
  
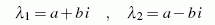  zusammengefasst werden. Dies liefert mit
  
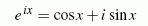  nach einem kurzen Ausflug in die Welt der komplexen Zahlen wieder relle Lösungsanteile.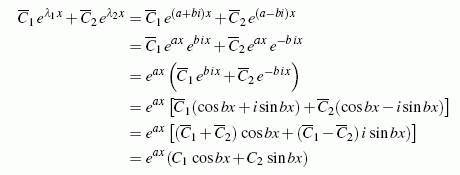
• Bei der Lösung der charakteristischen Gleichung treten mehrfache Nullstellen λ₁ = λ₂ = λ₃ = ... auf: Dies führt auf ein Defizit im Fundamentalsystem, das sich leicht beheben lässt. In diesem Fall gibt es weitere (linear unabhängige) Partikulärlösungen
  

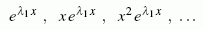
Hier findet man ausführlich vorgerechnete Beispiele der allgemeinen Lösung homogener linearer Differenzialgleichungen mit konstanten Koeffizienten:

• Die Verformung elastisch gebetteter Träger wird durch eine Differenzialgleichung 4. Ordnung beschrieben.
• Die freien Schwingungen einer durch eine Feder gefesselten Masse unter Berücksichtigung von (geschwindigkeitsproportionaler) Dämpfung wird durch eine Differenzialgleichung 2. Ordnung beschrieben.

Inhomogene lineare Differenzialgleichungen mit konstanten Koeffizienten

Die Lösung der inhomogenen linearen Differenzialgleichung n-ter Ordnung mit konstanten Koeffizienten

erfolgt in zwei Schritten:

• Die zugehörige homogene Differenzialgleichung (Störglied r(x) wird gleich Null gesetzt) wird so gelöst, wie es oben beschrieben wurde.
• Für die inhomogene Differenzialgleichung muss eine Partikulärlösung gefunden werden, an die keine weitere Forderung als die Erfüllung der Differenzialgleichung geknüpft wird (es darf irgendeine beliebig einfache Funktion sein, die diese Bedingung erfüllt).

Für die wichtigsten Störglieder gibt es Strategien, mit denen man zu einer solchen Partikulärlösung kommt: Es wird ein geeigneter Ansatz mit Freiwerten gewählt und in die inhomogene Differenzialgleichung eingesetzt. Dann werden die Freiwerte so bestimmt, dass die Differenzialgleichung erfüllt ist. Die folgende Tabelle zeigt für einige Störfunktionen r(x) die geeigneten Ansätzen für das Suchen nach einer Partikulärlösung y_part(x):

Störfunktion r(x)	Ansatz für ypart(x)
Polynom vom Grad m:  b0 + b1x + ... + bm xm	Polynom vom gleichen Grad m:  B0 + B1x + ... + Bm xm
e-Funktion mit dem Exponenten ax:  Aea x	e-Funktion mit dem gleichen Exponenten ax:  Bea x
Sinusfunktion mit dem Argument ax:  A sin ax	Linearkombination aus Sinus- und Cosinusfunktion mit dem gleichen Argument ax: B1 sin ax + B2 sin ax oder Ansatz mit den beiden Freiwerten B1 und φ0: B1 cos(ax+φ0)
Cosinusfunktion mit dem Argument ax:  A cos ax
Linearkombination aus Sinus- und Cosinusfunktion mit dem Argument ax:  A sin ax + B sin ax

Diese Ansätze versagen, wenn sie selbst die homogene Differenzialgleichung erfüllen (dann bleibt beim Einsetzen auf der linken Seite nichts übrig). In diesen Fällen führen die um den Faktor x erweiterten Ansätze zum Erfolg (gegebenenfalls muss man analog zum Vorgehen bei mehrfachen Nullstellen der charakteristischen Gleichung den Partikulärlösungsansatz um x², x³ usw. erweitern.

Hier findet man ausführlich vorgerechnete Beispiele der allgemeinen Lösung inhomogener linearer Differenzialgleichungen mit konstanten Koeffizienten:

• Die Verformung elastisch gebetteter Träger wird durch eine Differenzialgleichung 4. Ordnung beschrieben.
• Die erzwungenen Schwingungen einer durch eine Feder gefesselten Masse unter Berücksichtigung von (geschwindigkeitsproportionaler) Dämpfung wird durch eine Differenzialgleichung 2. Ordnung beschrieben.