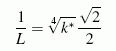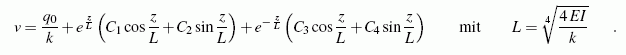Lineare Dgln. mit konstanten Koeffizienten

Aufgabe

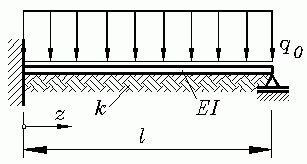
Der skizzierte elastisch gebetteten Träger mit konstanter Biegesteifigkeit EI auf einem Untergrund mit konstanter Bettungsziffer k trägt eine konstante Linienlast q₀. Im Kapitel "Spezielle Biegeprobleme wird für die Berechnung der vertikalen Durchbiegung des Trägers die Differenzialgleichung hergeleitet:

Die allgemeine Lösung dieser linearen Differenzialgleichung 4. Ordnung mit konstanten Koeffizienten setzt sich aus der allgemeinen Lösung der zugehörigen homogenen Differenzialgleichung und einer Partikulärlösung der inhomogenen Differenzialgleichung entsprechend zusammen. In die homogene Differenzialgleichung wird der für homogene lineare Differenzialgleichungen mit konstanten Koeffizienten passende Ansatz v = e^λz (v'''' = λ⁴e^λz) eingesetzt. Die auf diese Weise gewonnene charakteristische Gleichung 4. Grades hat vier verschiedene komplexe Lösungen Wie man sich leicht überzeugt, hat der gemeinsame Faktor der vier Lösungen die Dimension ("Länge")^-1. Deshalb wird die Abkürzung eingeführt, so dass die vier λ-Werte in der Form aufgeschrieben werden können. λ₁ und λ₂ sind zueinander konjugiert komplex, ebenso λ₃ und λ₄. Deshalb können jeweils die beiden zugehörigen (komplexen) Partikulärlösungen zusammengefasst werden, wie es hier allgemein demonstriert wurde. Damit lautet die Lösung der homogenen Differenzialgleichung: Schließlich muss noch eine Partikulärlösung für die inhomogene Differenzialgleichung gefunden werden, was in diesem Fall "durch genaues Hinsehen" erledigt werden kann. Polynomfunktionen bis 3. Grades verschwinden bei der 4. Ableitung, so dass für eine Partikulärlösung nur der zweite Summand auf der linken Seite betrachtet werden muss. Es ist klar, dass für diese Polynomfuntionen (und natürlich erst recht für die in diesem Fall konstante rechte Seite) die Differenzialgleichung für erfüllt ist. Damit ist nun auch die allgemeine Lösung der Differenzialgleichung für die Differenzialgleichung des elastisch gebetteten Trägers bekannt:

Spezielle Lösung der Differenzialgleichung

Die allgemeine Lösung enthält 4 Integrationskonstanten. Um daraus die spezielle Lösung für das aktuelle Problem zu erzeugen, müssen 4 Randbedingungen formuliert werden. Am linken (starr eingespannten) Rand ist die Vertikalverschiebung gleich Null, und die Biegelinie muss eine horizontale Tangente haben. Am rechten Rand ist die Vertikalverschiebung ebenfalls Null, außerdem ist dieser Rand biegemomentenfrei.

Die Berechnung der Integrationskonstanten aus diesen Bedingungen ist mit einigem Aufwand verbunden, die Hilfe des Computers ist dringend anzuraten. Man findet die komplette Rechnung und die Auswertung der Ergebnisse hier.