Lineare Unabhängigkeit von Funktionen

Lineare Abhängigkeit bzw. Unabhängigkeit

Beispiel: Die Funktionen f₁(x) = x², f₂(x) = e^x und f₃(x) = e^-x sind linear unabhängig, weil man kein Konstanten-Tripel C₁, C₂, C₃ finden kann, das ihre Linearkombination verschwinden lässt, es sei denn, alle drei Konstanten sind Null.

Die drei Funktionen f₁(x) = cosh x, f₂(x) = e^x und f₃(x) = e^-x sind dagegen linear abhängig, weil eine Linearkombination mit C₁ = 1, C₂ = 0,5 und C₃ = 0,5 entsprechend

identisch Null ist.

Prüfen der linearen Unabhängigkeit von Funktionen, Wronskische Determinante

Die oben formulierte Beziehung, die erfüllt sein muss, wenn n Funktionen f_i(x) linear abhängig sind, wird (n−1)-mal abgeleitet:

Dies ist ein homogenes lineares Gleichungssystem für die C_i das nur dann nichttriviale Lösungen (nicht alle C_i sind gleich Null) haben kann, wenn seine Koeffizientendeterminante gleich Null ist. Das führt zu folgendem Schluss:

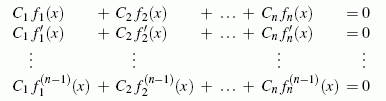
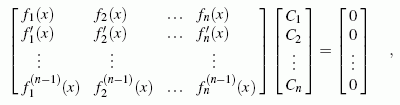
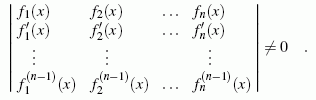
Beispiel 1: Für die bereits oben behandelten drei Funktionen f₁(x) = cosh x, f₂(x) = e^x und f₃(x) = e^-x ergibt sich die Wronskische Determinante

bei der man sofort erkennt, dass sie den Wert Null hat, weil die erste und die dritte Zeile der Determinante gleich sind (zu den Regeln zur Berechnung von Determinanten siehe "Determinanten n-ter Ordnung"). Die drei Funktionen sind also nicht linear unabhängig, wie oben bereits gezeigt wurde.

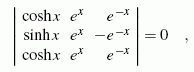
Beispiel 2: Für die homogene lineare Differenzialgleichung 2. Ordnung

sind die beiden Funktionen Partikulärlösungen, wie man sich durch Einsetzen leicht überzeugt. Die Überprüfung mit der Wronskischen Determinante ergibt: Die beiden Funktionen sind also linear unabhängig, so dass die allgemeine Lösung der Differenzialgleichung ist.