Aufgabe
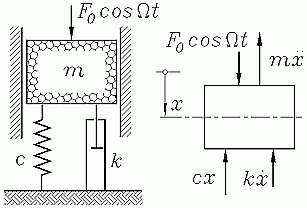
Eine Masse m ist wie skizzert durch eine Feder (Federzahl c) gefesselt. Sie wird durch die zeitlich veränderliche Kraft F0 cos Ωt zu Schwingungen angeregt (diese so genannte harmonische Erregung ist der praktisch wichtigste Fall, verursucht zum Beispiel durch eine Maschine mit einer mit der Winkelgeschwindigkeit Ω umlaufenden Unwucht).
Die Bewegung wird vertikal geführt und geschwindigkeitsproportional gedämpft (Dämpfer mit der Dämpfungskonstanten k). Sie wird durch eine lineare inhomogene Differenzialgleichung 2. Ordnung mit konstanten Koeffizienten beschrieben, deren allgemeine Lösung berechnet werden soll.
Die Schnittskizze zeigt die vier angreifenden Kräfte (es wurde der in der Technischen Mechanik übliche "Trick" genutzt, das Eigengewicht der Masse mg und die dadurch hervorgerufene Federvorspannung wegzulassen, weil die beiden Kräfte während des gesamten Bewegungsvorgangs für sich ein Gleichgewichtssystem bilden, x = 0 ist also die statische Ruhelage des Systems). Aus dem Gleichgewicht der Kräfte resultiert die Differenzialgleichung
| Klicken auf die Animation wechselt zur interaktiven Seite "Unwuchterregter Schwinger". |
Die beiden Lösungsanteile werden nachfolgend berechnet.
Lösung der homogenen Differenzialgleichung
Die homogene Differenzialgleichung
Die allgemeine Lösung dieser Differenzialgleichung findet man mit dem Exponentialansatz x = e λt, der eine charakteristische Gleichung liefert, deren Lösungen reell oder komplex sein können:
- Starke Dämpfung: Für
D > 1
ergeben sich zwei reelle und voneinander verschiedene
λ-Werte, und die Lösung kann in der Form
aufgeschrieben werden. Der Faktor vor der Klammer sorgt dafür, dass sich x asymptotisch dem Wert Null nähert.
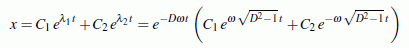
- Aperiodischer Grenzfall:
D = 1 führt
auf ein Defizit im Fundamentalsystem, das sich leicht
beheben lässt. Hier wird beschrieben,
wie man in diesem Fall weitere linear unabhängige Partikulärlösungen
findet. In diesem Fall lautet die Lösung:
Die beiden Fälle mit reellen λ-Werten sind von geringerem Interesse, weil sie keine Schwingungsvorgänge beschreiben. Sie sind manchmal erwünscht (zum Beispiel als Zeigerbewegungen in Messinstrumenten), werden aber hier zugunsten des folgenden deutlich wichtigsten Falls nicht weiter betrachtet.
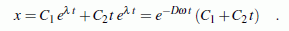
- Schwache Dämpfung: Für den Fall
D < 1 ergeben sich zwei
komplexe Lösungen für λ.
Die beiden Partikulärlösungen werden
(wie hier allgemein beschrieben)
mit Hilfe der Euler-Relation umgeformt, so dass reelle Funktionen
entstehen:
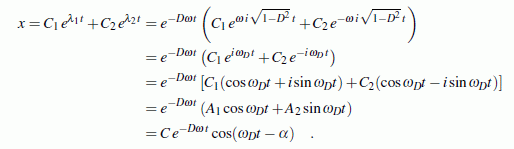
Aus diesem Ergebnis resultiert eine wichtige Erkenntnis:
Ein (geschwindigkeitsproportional) gedämpftes freies Schwingungssystem (keine Erregerkraft, einmal angeregt und sich selbst überlassen) schwingt mit konstanter Eigenfrequenz (bei abnehmenden Amplituden). Die Eigenkreisfrequenz der gedämpften Schwingung
Der Ingenieur registriert eine weitere wichtige Tatsache: Weil bei den weitaus meisten praktischen Schwingungsproblemen nur die Eigenkreisfrequenz von Interesse ist, braucht man die Differenzialgleichung gar nicht zu lösen. Wenn man die Parameter des Problems kennt, ist die Eigenkreisfrequenz bekannt.
Die Auswertung der Lösung der homogenen Differenzialgleichung, die die freie gedämpfte Schwingung beschreibt, findet man hier mit dem Programm Maple und dem Tischrechner TI und hier mit dem Programm Matlab.
Partikulärlösung für die inhomogene Differenzialgleichung
Die Störfunktion (Funktion auf der rechten Seite) der inhomogenen Differenzialgleichung
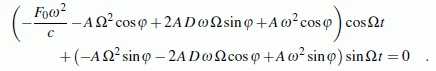
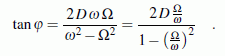
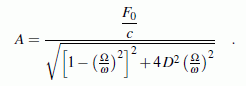
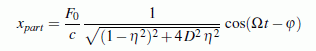
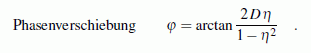
Lösung der inhomogenen Differenzialgleichung
Die Lösung der inhomogenen Differenzialgleichung
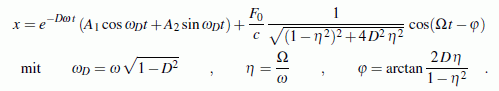
Lösung für spezielle Parameter, Analyse der Lösungsanteile
Unter der willkürlichen Annahme, dass die Bewegung zum Zeitpunkt t = 0 aus der Ruhe heraus beginnt, soll die Funktion x(t) für die beiden folgenden Sätze von Parametern ausgewertet werden. Diese sind so gewählt, dass die wichtigsten Erkenntnisse über den Einfluss der beiden Lösungsanteile gewonnen werden können:
- m = 150 kg ; F0 = 0,001 N ; Ω = 10 s-1 ; c = 12·105 N/m ; k = 250 kg/s ;
- m = 150 kg ; F0 = 0,001 N ; Ω = 10 s-1 ; c = 3 N/m ; k = 25 kg/s .
Für die Auswertung der Anfangsbedingungen wird neben der oben angegebenen Funktion x(t) auch deren erste Ableitung nach der Zeit benötigt:
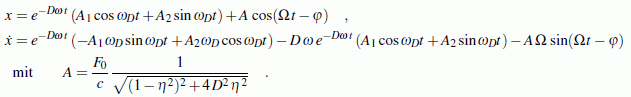
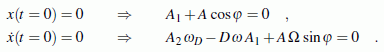
m = 150 ; F0 = 0.001 ; c = 12e5 ; k = 0.25e3 ; Omega = 10 ; tend = 6 ; xmax = 2e-9 ;
t = 0 : tend/1000 : tend ; % Auswertung fuer 1000 Zeitschritte
omega = sqrt(c/m) ;
eta = Omega/omega ;
D = k/(2*sqrt(m*c)) ;
phi = atan((2*D*eta)/(1-eta^2)) ;
if (phi < 0) phi = phi+pi ; end % phi muss im Bereich 0 .. pi liegen
omegaD = omega*sqrt(1-D^2) ;
A = F0/(c*sqrt((1-eta^2)^2+4*D^2*eta^2)) ;
A1 = - A*cos(phi) ;
A2 = - A*(D*omega*cos(phi)+Omega*sin(phi))/omegaD
xhom = exp(-D*omega*t).*(A1*cos(omegaD*t)+A2*sin(omegaD*t)) ;
xpart = A*cos(Omega*t-phi) ;
x = xhom + xpart ;
str = ['x(t) für \omega = ' , num2str(omega) , ' und \Omega = ' , num2str(Omega)] ;
subplot(2,1,1) ; plot (t , x) , grid on , title (str) , axis([0 tend -xmax xmax])
subplot(2,1,2) ; plot (t , xpart , t , xhom , 'r') , grid on ,
title ('Blau: x_{part}(t) = x_{st}(t) , Rot: x_{hom}(t)') , axis([0 tend -xmax xmax])
Für den im Script realisierten Fall a mit einer relativ harten Feder genügt die Verfolgung des Bewegungsablaufs über nur 6 Sekunden, um die wesentlichen Erkenntnisse zu gewinnen. Nachfolgend ist im oberen Graphikfenster das Bewegungsgesetz x(t) zu sehen, darunter die beiden Anteile xhom(t) und xpart(t). Man sieht sehr schön, wie die (rot gezeichnete) Eigenschwingung infolge der Dämpfung abklingt, so dass sich sehr bald eine Schwingung einstellt, die ausschließlich durch die Partikulärlösung der Differenzialgleichung beschrieben wird:
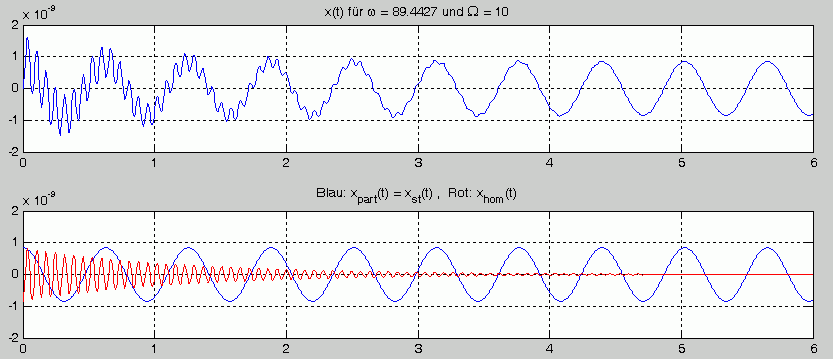
Der oben zu sehende Schwingungsverlauf ist typisch für den Fall, dass die Eigenkreisfrequenz des freien (ungedämpften) Schwingers größer ist als die Erregerkreisfrequenz (ω > Ω): Die kurzwelligen Eigenschwingungen überlagern anfangs die langwelligeren erzwungenen Schwingungen, klingen infolge der Dämpfung aber ab, so dass die Kurve immer glatter wird.
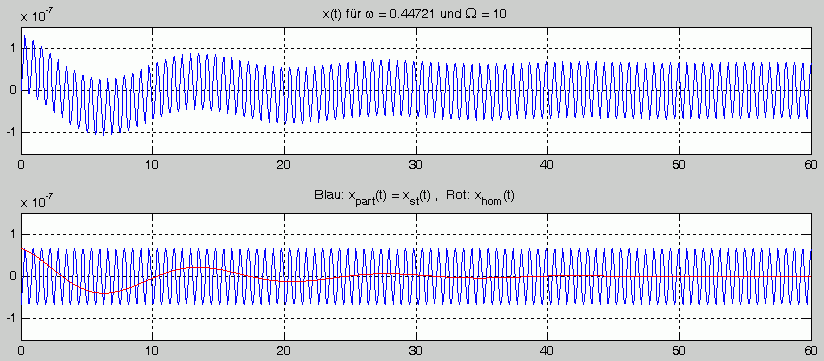
Auch wenn sich für den entgegengesetzten Fall (ω < Ω) der Kurvenverlauf deutlich anders darstellt, ist der Effekt gleich: Die erzwungenen Schwingungen bewegen sich anfangs kurzwellig um die langwelligen Eigenschwingungen. Letztere klingen ab, und es verbleibt die durch die Partikulärlösung beschriebene erzwungene Schwingung. Die Ergebnisse der Berechnung mit den Parametern des Falls b zeigen dies, wenn man den Bewegungsverlauf etwa 60 Sekunden lang verfolgt:
Weiteres Beispiel
Das nebenstehend skizzierte Schwingungsproblem (die Fundamentschwingungen sollen getilgt werden) wird für eine Teilaufgabe auf der Basis der hier entwickelten theoretischen Grundlagen gelöst.
Zusammenfassung der Erkenntnisse
Die mit der Lösung der Schwingungs-Differenzialgleichung theoretisch gefundenen Erkenntnisse lassen sich mit den am Beispiel demonstrierten Fällen zu folgenden Aussagen zusammenfassen:
Stationäre Lösung: Nach einer bestimmten Einschwingzeit schwingt der durch die harmonisch veränderliche Kraft F0 cos Ωt erregte gedämpfte Schwinger nach einem Bewegungsgesetz, das nur noch durch die Partikulärlösung der Bewegungs-Differenzialgleichung bestimmt wird. Dieses heißt deshalb stationäre Lösung:
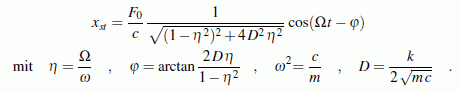
Die Schwingung im stationären Zustand erfolgt mit der Erregerkreisfrequenz Ω. Die Amplitude der stationären Schwingung ist konstant.
Die Größe der Amplitude (Ausdruck vor der cos-Funktion) wird wesentlich vom Abstimmungsverhältnis η (Quotient von Erregerkreisfrequenz Ω und Eigenkreisfrequenz ω des ungedämpften Schwingers) bestimmt.
- Im Ausdruck für die Amplitude der stationären Schwingung steht mit
ein Faktor, der die Auslenkung der Feder infolge einer (konstanten) statischen Last F0 beschreibt. Mit dem zweiten Faktor (Bruch, der nur vom Abstimmungsverhältnis und der Dämpfung abhängig ist) wird also bestimmt, ob sich im dynamischen Fall die Amplitude gegenüber dem statischen Fall verkleinert oder vergrößert. Deshalb wird der Ausdruck
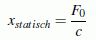Vergrößerungsfunktion genannt.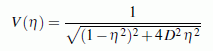
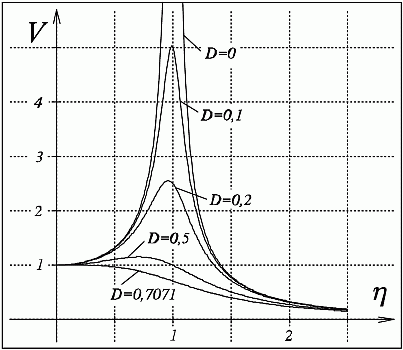
- Die nebenstehende Graphik zeigt die Vergrößerungsfunktionen für verschiedene Dämpfungswerte. Alle Kurven haben zwei gemeinsame Eigenschaften: Für sehr kleine η-Werte (sehr kleine Erregerfrequenz Ω) ist V nahe bei 1 (Kraftwechsel erfolgt so langsam, dass die Masse der Kraft einfach folgt, ohne dass sich eine echte Schwingung zeigt). Für sehr große η-Werte (sehr große Erregerfrequenz Ω) werden die V-Werte sehr klein (Kraftwechsel erfolgt so schnell, dass die Masse "kaum folgen kann").
- Bei sehr kleiner Dämpfung nimmt die Vergrößerungsfunktion
in der Nähe von η = 1
sehr große Werte an (für D = 0 hat sie
bei η = 1 eine Polstelle):
Eine Erregung mit einer Kreisfrequenz Ω, die der Eigenkreisfrequenz ω des ungedämpften Schwingers entspricht, führt bei kleiner Dämpfung zu sehr großen Amplituden (Resonanz). - Weil alle Vergrößerungsfunktionen für η > 1 gegen Null streben, ist dieser so genannte überkritische Bereich (Ω = ω wird als kritische Erregerkreisfrequenz bezeichnet) dann als Arbeitsbereich für Maschinen bevorzugen, wenn Schwingungen vermieden bzw. weitgehend reduziert werden sollen. Dies ist bis auf wenige Ausnahmen (z. B.: Schwingsiebe) der Regelfall.
Zum Schluss gibt es noch zwei angenehme Informationen für Ingenieure:
- Resonanz muss entweder vermieden werden (typischer Fall) oder ist erwünscht (Beispiel: Schwingsieb). Beides ist ohne Rechnung zu beurteilen, wenn man die Parameter kennt: Man muss nur die Erregerkreisfrequenz mit der Eigenkreisfrequenz des ungedämpften Schwingers vergleichen, die man bei bekannten Werten für c und m ohne große Rechnung sofort aufschreiben kann.
- Für Arbeitsmaschinen im Dauerbetrieb ist die Arbeit im überkritischen Bereich zu bevorzugen (nur beim Hochfahren und beim Abbremsen muss der kritische Bereich möglichst kurzzeitig durchlaufen werden). Wo dieser Bereich liegt, ist aber auch mit der Kenntnis der beiden Kreisfrequenzen Ω und ω bekannt. Mit der Vergrößerungsfunktion kann man dann gegebenenfalls noch die Größen der Amplituden für die aktuelle Erregerkreisfrequenz Ω bestimmen.
Die gute Nachricht lautet also: Nachdem man einmal die hier demonstrierte Lösung der Schwingungs-Differenzialgleichung nachempfunden hat (das allerdings ist schon empfehlenswert), braucht man in der Praxis nur die Ergebnisse dieser Rechnung an das aktuelle Problem anzupassen.
