Differenzialgleichungen 1. Ordnung

Das Problem

Die Aufgabe, die Funktion y(x) zu bestimmen, die einen Spiegel definiert, der paralleles Licht so ablenkt, dass sich alle Lichtstrahlen in einem Punkt (Fokus) treffen, kann ohne Einschränkung der Allgemeinheit für Lichtstrahlen parallel zur x-Achse und mit dem Nullpunkt als Fokus formuliert werden.

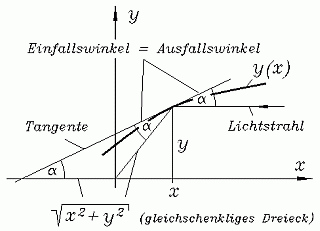
Einige einfache geometrische Überlegungen (Seiten gleicher Länge im Dreieck, das wegen der gleichen Basiswinkel α gleichschenklig ist, nebenstehende Skizze) führen auf die Differenzialgleichung

bzw. nach Division durch x im Zähler und Nenner der rechten Seite: (nichtlineare gewöhnliche Differenzialgleichung 1. Ordnung). Dies ist eine so genannte "Ähnlichkeits-Differenzialgleichung" y' = f(y/x). Differenzialgleichungen dieses Typs lassen sich mit der Transformation u = y/x lösen, was nachfolgend demonstriert wird.

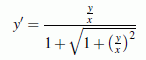
Lösung der Ähnlichkeits-Differenzialgleichung

Mit der oben genannten Transformation und der zugehörigen Ableitung

entsteht eine Differenzialgleichung, bei der die Variablen getrennt werden können (hier: x nach links, u nach rechts): Nun kann auf beiden Seiten integriert werden: Das Integral auf der linken Seite ist ein Grundintegral, das Integral auf der rechten Seite macht etwas mehr Schwierigkeiten. Auch hier hilft eine Transformation. Mit berechnet man: Nun kann die Lösung der transformierten Differenzialgleichung aufgeschrieben werden. Weil auf beiden Seiten bei der Integration der natürliche Logarithmus entstand, werden auch die beiden Integrationskonstanten zweckmäßig zur Konstanten lnC zusammengefasst: Dies lässt sich noch vereinfachen: Die beiden Rücktransformationen führen über zur allgemeinen Lösung der Differenzialgleichung: Die allgemeine Lösung ist eine Schar quadratischer Parabeln, die alle die Forderungen der Aufgabenstellung erfüllen. Mit der Festlegung eines beliebigen Punktes, durch den die Lösungsfunktion gehen soll, kommt man zu einer speziellen Lösung. Die Forderung, dass zum Beispiel der Punkt (0;1) zur Lösungskurve gehören soll, liefert nach Einsetzen in die allgemeine Lösung für die Konstante C neben dem uninteressanten Wert 0 die Lösung C = 1. Damit erhält man die "Spiegel-Funktion" (Parabolspiegel):

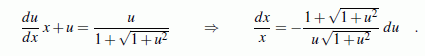
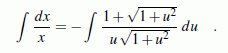
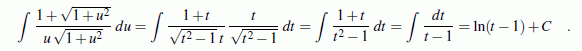
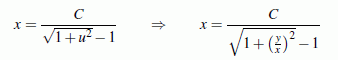
Fazit

Das ist natürlich "schöne Mathematik": Mit einer geeigneten Transformation wird eine nichtlineare Differenzialgleichung in eine Form überführt, die nach Trennung der Variablen eine geschlossene Integration ermöglicht. Aber in der Regel entstehen auch nach der Trennung der Variablen keine Integrale, die sich (wie bei diesem Beispiel wieder mit Hilfe einer Transformation) geschlossen lösen lassen.

Dass auf der Internet-Site "Mathematik für die Technische Mechanik" hier auf ein Beispiel aus der Optik zurückgegriffen wurde, deutet auf ein anderes Dilemma: In der Technischen Mechanik gibt es kaum Differenzialgleichungen 1. Ordnung, aber leider sehr viele nichtlineare Differenzialgleichungen höherer Ordnung, die bis auf wenige "akademische Probleme" nicht geschlossen lösbar sind. Diese werden auf der Seite "Numerische Integration von Anfangswertproblemen" ausführlich behandelt. Dort findet man als Einführungsbeispiel im Skript "Numerische Integration von Anfangswertproblemen - Teil 1: Grundlagen" auch das hier behandelte "Spiegel-Problem" wieder, weil damit ein Vergleich der numerischen mit der exakten Lösung der Differenzialgleichung möglich ist.