Allgemeine Form der linearen Differenzialgleichung
Eine Lineare Differenzialgleichung n-ter Ordnung
Die Funktion r(x) auf der rechten Seite wird auch "Störglied" genannt (und ist bei der Lösung tatsächlich störend). Wenn diese Funktion identisch Null ist, nennt man
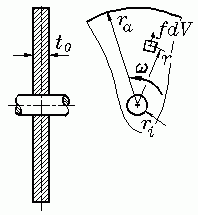
Beispiel: Für die Berechnung der Radialspannungen in einer mit der Winkelgeschwindigkeit ω rotierenden Kreisringscheibe wird im Kapitel "Rotationssysmmetrische Modelle" die Differenzialgleichung hergeleitet:
Die zu dieser Differenzialgleichung gehörende homogene Differenzalgleichung
Homogene lineare Differenzialgleichungen
Jede Funktion y(x), die die homogene lineare Differenzialgleichung
eine Lösung dieser homogen Differenzialgleichung.
Beispiel 1: Die Bewegung der als
Einführungsbeispiel
behandelten freien Schwingung einer Masse m,
die durch eine Feder (mit der Federzahl c) gefesselt ist,
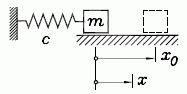 wird durch die homogene lineare Differenzialgleichung zweiter Ordnung
wird durch die homogene lineare Differenzialgleichung zweiter Ordnung
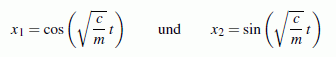
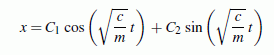
Beispiel 2: Die homogene lineare Differenzialgleichung
In beiden Beispielen sind die Linearkombinationen der beiden Partikulärlösungen sogar die allgemeinen Lösungen, weil die folgenden allgemeinen Kriterien erfüllt sind:
Die Lösung einer homogenen linearen Differenzialgleichung n-ter Ordnung
ist die Linearkombinationen von genau n Partikulärlösungen.
Diese müssen
- die Differenzialgleichung erfüllen und
- linear unabhängig sein. "Linear unabhängig" heißt, dass keine der Funktionen
sich als Linearkombination der anderen Funktionen darstellen lässt.
Diesem etwas schwierigen
Begriff ist eine eigene Seite gewidmet.
Die n Partikulärlösungen, die die genannten Kriterien
erfüllen, bilden für die Differenzialgleichung ein so genanntes
"Fundamentalsystem".
Damit sind die Kriterien bekannt, die die allgemeine Lösung einer homogenen linearen Differenzialgleichung erfüllen müssen. Die Frage, wie man die Funktionen findet, die ein Fundamentalsystem bilden, kann leider nicht allgemein beantwortet werden. Für einige spezielle Typen können erfolgversprechende Strategien formuliert werden. Dazu gehören zum Beispiel die für die Technische Mechanik sehr wichtigen "Linearen Differenzialgleichungen mit konstanten Koeffizienten" und die "Eulersche Differenzialgleichung".
Inhomogene lineare Differenzialgleichungen
Es gilt die folgende wichtige Aussage:
Für die Lösung einer linearen Differenzialgleichung sind also zwei Schritte erforderlich:
- Es ist die allgemeine Lösung der zugehörigen homogenen Differenzialgleichung zu finden, die entsteht, wenn man das Störglied r(x) Null setzt. Dass dies in der Regel nicht ganz einfach ist, wurde oben beschrieben.
- Es muss eine beliebige (wenn auch noch so simple) Lösung für die inhomogene Differenzialgleichung gefunden werden. Auch dafür gibt es leider kein allgemeingültiges Rezept. Manchmal findet man durch "scharfes Ansehen" der Differenzialgleichung schon eine solche Lösung (sie darf ja beliebig einfach sein). Für eine ganze Reihe typischer Störglieder r(x) bieten sich Ansätze mit einem freien Parameter an, den man durch Einsetzen in die Differenzialgleichung bestimmen kann.
Beispiel: Für die als Eingangsbeispiel angegebene lineare Differenzialgleichung für die Berechnung der Radialspannungen in einer rotierenden Scheibe
Anwendungen, Beispiele
- Dem Spezialfall
"Lineare Differenzialgleichungen mit konstanten Koeffizienten"
ist eine eigene Seite gewidmet.
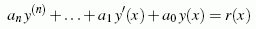
- Ein in der Technischen Mechanik häufig auftretender Fall sind
Differenzialgleichungen der Form
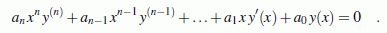
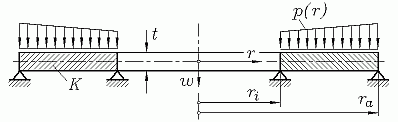 Diese werden auf der Seite
"Eulersche Differenzialgleichungen" ausführlich behandelt.
Eine Differenzialgleichung dieses Typs 2. Ordnung wurde
bereits hier als Einführungsbeispiel
vorgestellt.
Eine Eulersche Differenzialgleichung 4. Ordnung wird auf der Seite
"Rotationssymmetrische Kreis- und Kreisringplatten"
vorgestellt (nebenstehndes Bild), ein komplett durchgerechnetes Beispiel findet man auf der Seite
"Rotationssymmetrische Kreisringplatte, Beispiel".
Diese werden auf der Seite
"Eulersche Differenzialgleichungen" ausführlich behandelt.
Eine Differenzialgleichung dieses Typs 2. Ordnung wurde
bereits hier als Einführungsbeispiel
vorgestellt.
Eine Eulersche Differenzialgleichung 4. Ordnung wird auf der Seite
"Rotationssymmetrische Kreis- und Kreisringplatten"
vorgestellt (nebenstehndes Bild), ein komplett durchgerechnetes Beispiel findet man auf der Seite
"Rotationssymmetrische Kreisringplatte, Beispiel".
- Im allgemeinen Fall sind auch die linearen Differenzialgleichungen nicht geschlossen lösbar. Da aber die Probleme der Technischen Mechanik eigentlich immer als Randwertprobleme formuliert sind, ist das Differenzenverfahren die universell anwendbare Lösungsstrategie.

