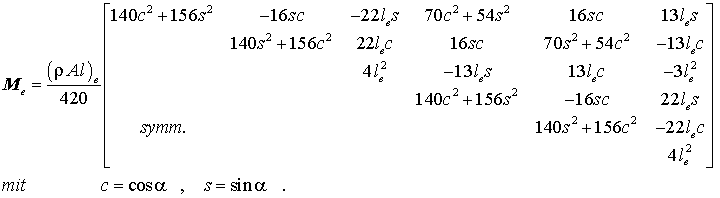Ebenes Rahmenelement
Ein ebener Rahmen besteht aus biege- und dehnsteifen Elementen, die Normalkräfte, Querkräfte und Biegemomente übertragen können.
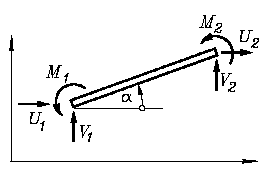
Deshalb ist das einfachste finite Element, das für diese Problemklasse definiert werden kann, eine Kombination aus Zug-Druck-Stab und geradem Biegeträger mit zwei Knoten, an denen jeweils drei Knotenlasten angreifen (Skizze links). Entsprechend dem üblichen Vorgehen bei der Finite-Elemente-Methode werden diese für alle Elemente und an jeweils beiden Knoten mit gleichen Richtungen definiert. Gleichzeitig werden für alle Knoten analoge Verformungen (hier also zwei Verschiebungen und ein Biegewinkel) mit gleichen positiven Richtungen festgelegt.
Das ebene Rahmenelement hat sechs Freiheitsgrade, jeder Knoten hat drei Freieheitsgrade.
Globale und lokale Koordinaten
Die Geometrie (Koordinaten der Knoten) eines ebenen Rahmens wird in einem beliebig zu definierenden globalen Koordinatensystem beschrieben. Für die Betrachtung des einzelnen Elements ist dafür nur bedeutsam,
- dass sich für alle Elemente die Elementknotenkräfte U1, V1, U2 und V2 auf diese Koordinatenrichtungen beziehen (die Momente M1 und M2 an den Knoten werden linksdrehend positiv definiert),
- dass positive Knotenverschiebungen (und positive Biegewinkel) genau die Richtungen der Kräfte (bzw. Momente) haben und
- dass mit den Koordinaten der beiden zum Element gehörenden Knoten auch dessen Länge le bekannt ist.
Die zu entwickelnden Elementmatrizen Ke und Me müssen sich auf diese Element-Knotenlasten und Element-Knotenverformungen beziehen.
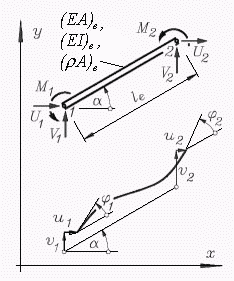
Zur Vereinfachung der Betrachtungen werden aber zunächst Knotenlasten und -verformungen verwendet, deren Richtungen mit der Längsachse des Elements zusammenfallen bzw. senkrecht dazu gerichtet sind. Diese werden jeweils mit einem Querstrich über dem Symbol gekennzeichnet.
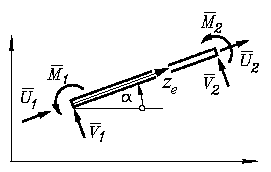
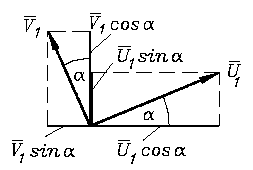
Die Skizze links zeigt dies für die Knotenlasten (für die Verformungen gelten die gleichen Richtungen). Es wird außerdem eine dem Element zugeordnete lokale Koordinate ze eingeführt, mit der die Elementbetrachtungen nach den vertrauten Beziehungen für den geraden Zug-Druck-Stab bzw. den geraden Biegeträger durchgeführt werden.
Die Skizze rechts verdeutlicht, wie man zur Rückrechnung auf die globalen Richtungen die Kräfte mit den lokalen Richtungen in Kompononten zerlegen muss, und es wird vorbereitend für die Rückrechnung schon einmal der Zusammenhang zwischen den unterschiedlich gerichteten Knotenkräften formuliert. Für den Knoten 1 des Elements liest man ab (die Beziehung für die Momente ist trivial):
![]()
In Matrixform lässt sich diese Beziehung der Knotenlasten des Knotens 1 also so formulieren:
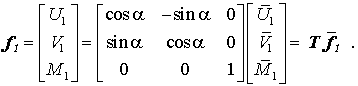
Natürlich gilt am Knoten 2 eine analoge Transformationsbeziehung mit der gleichen Transformationsmatrix T, so dass sich der gesamte Vektor der sechs Elementbelastungen von den lokalen auf die globalen Richtungen folgendermaßen transformieren lässt:
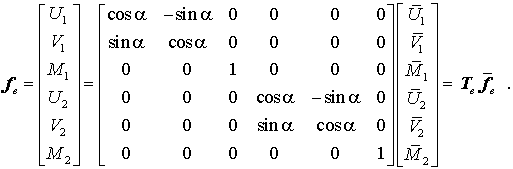
Es ist selbstverständlich, dass eine entsprechende Beziehung mit der gleichen Transformationsmatrix Te für die Knotenverformungen des Elements gilt:
![]()
Wenn also eine Beziehung zwischen den Knotenlasten und den Knotenverformungen in einem der beiden Systeme bekannt ist, kann diese auf das anderen System umgerechnet werden, z. B. wird aus
![]()
(mit Kräften und Verschiebungen in den "Element-Richtungen") durch Einsetzen der Transformationsbeziehungen:
![]()
Diese Beziehung vereinfacht sich noch dadurch, dass Te eine so genannte Orthonormalmatrix ist (es wird von einem rechtwinkligen System in ein anderes rechtwinkliges System transformiert). Für Orthonormalmatrizen gilt, dass ihre Inverse gleich ihrer Transponierten ist.
Bei den Betrachtungen zu den "Grundgleichungen der Finite-Elemente-Methode (Eigenschwingungen elastischer Systeme)" wird deutlich, dass beim Übergang auf andere Richtungen auf die Massenmatrizen die gleichen Transformationen wie auf die Steifigkeitsmatrizen angewendet werden müssen, und damit ist die Strategie klar. Die Elementsteifigkeitsmatrix und die Elementmassenmatrix werden zunächst im wesentlich einfacheren "Querstrich-System" entwickelt und danach folgendermaßen auf die globalen Richtungen transformiert:
![]()
Ansatzfunktionen
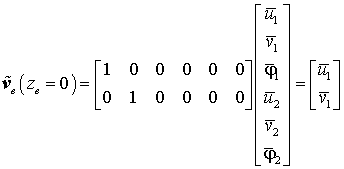
Für die Biegeverformung können die Ansatzfunktionen übernommen werden, die für den geraden Biegeträger hergeleitet wurden. Für die Verformung in Längsrichrichtung des Elements kann nur ein linearer Ansatz verwendet werden, weil nur zwei Knotenverschiebungen in dieser Richtung vorgesehen sind. Der folgende Ansatz erfüllt die Bedingungen, an den Knoten beim Einsetzen der Koordinate ze (0 für den Knoten 1 und le für den Knoten 2) die Knotenverformungen zu liefern:
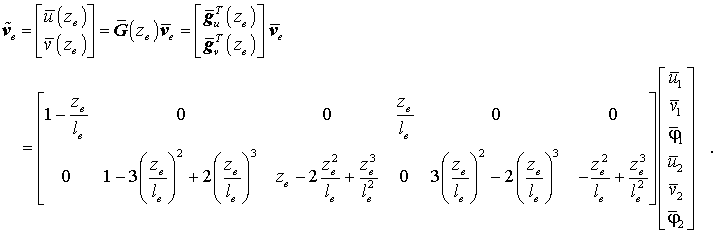
Es ist sofort zu sehen, dass z. B.
 und
und
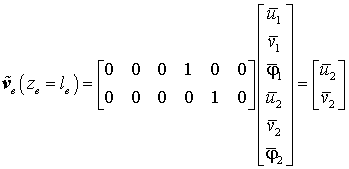
gilt.
Elementsteifigkeitsmatrix
Das für den reinen Biegeträger formulierte elastische Potenzial muss um den Anteil aus den Längsverschiebungen erweitert werden und kann z. B. so formuliert werden:
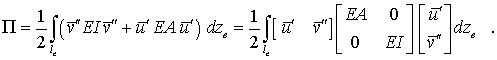
Mit den Ableitungen der Ansatzfunktionen
![]()
erhält man (die Skalarprodukte sind auch in umgekehrter Reihenfolge bei Vertauschen des Transponiersymbols aufschreibbar):
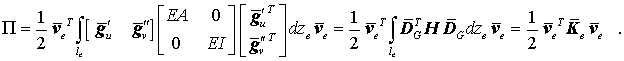
In dieser Beziehung steckt die (auf das "Querstrich-System" bezogene) Elementsteifigkeitsmatrix
![]()
mit
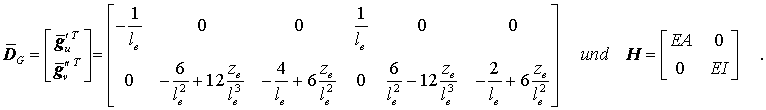
Nach dieser Vorschrift kann also die auf das "Querstrich-System" bezogene Elementsteifigkeitsmatrix berechnet werden, die dann entsprechend
![]()
mit der oben angegebenen Transformationsmatrix auf die globalen Richtungen transformiert werden muss.
Sonderfall: Konstante Biege- und Dehnsteifigkeit
Für den wichtigen Spezialfall konstanter Biege- und Dehnsteifigkeit kann die oben angegebene Integralformel für die Berechnung der Elementsteifigkeitsmatrix im "Querstrich-System" mit etwas Mühe "von Hand" ausgewertet werden (zur Erinnerung: Matrizen werden integriert, indem jedes einzelne Element integriert wird). Man erhält:
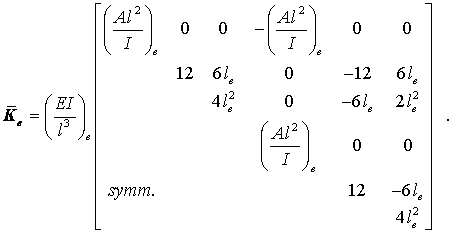
Auch die Transformation auf die globalen Richtungen nach der oben angegebenen Formel mit der ebenfalls hergeleiteten Transformationsmatrix Te gelingt. Man erhält die
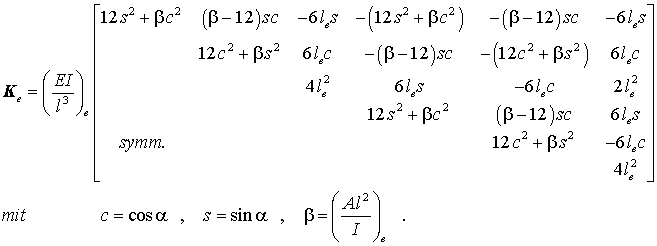
Elementmassenmatrix
Nach diesen Vorarbeiten kann die Elementmassenmatrix direkt nach der auf der Seite "Grundgleichungen der Finite-Elemente-Methode (Eigenschwingungen elastischer Systeme)" angegebenen Formel berechnet werden:
![]()
mit
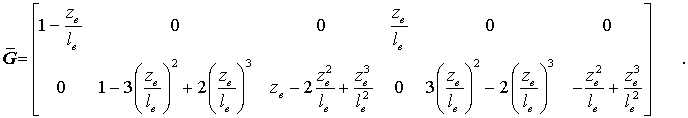
Auch die auf das "Querstrich-System" bezogene Elementmassenmatrix muss entsprechend
![]()
auf die globalen Richtungen umgerechnet werden.
Sonderfall: Konstante Massebelegung
Für den wichtigen Spezialfall konstanter Massebelegung kann auch die oben angegebene Integralformel für die Berechnung der Elementmassenmatrix im "Querstrich-System" mit etwas Mühe "von Hand" ausgewertet werden. Man erhält:
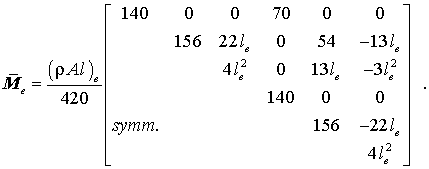
Auch die Transformation auf die globalen Richtungen nach der oben angegebenen Formel mit der ebenfalls hergeleiteten Transformationsmatrix Te gelingt. Man erhält die