Das Problem
Obwohl jede analytisch aufschreibbare Funktion nach den hier zusammengestellten "Ableitungsregeln" differenziert werden kann, gibt es (zum Beispiel wegen des Aufwands) häufig Gründe, numerisch zu differenzieren. Insbesondere für die numerische Lösung von linearen Randwertproblemen werden die Formeln benötigt, nach der für einen Punkt einer Funktion die Ableitungen numerisch berechnet werden können.
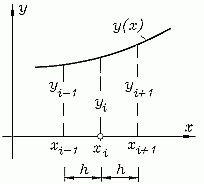
Betrachtet wird die Umgebung der Stelle xi, für die die Ableitung der Funktion y(x) berechnet werden soll, speziell die beiden Nachbarpunkte xi−1 und xi+1, die sich jeweils im Abstand h von xi befinden (nebenstehende Skizze). Nach der auf der Seite "Differenzen- und Differenzialquotient" gegebenen Definition
![]()
kann die Ableitung von y(x) sinnvoll auf zwei Wegen genähert werden:
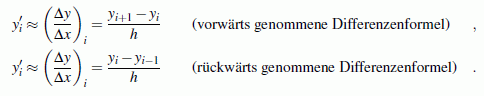
Beide Näherungswerte sind mit einem Fehler behaftet, der umso kleiner ist, je kleiner h ist. Wenn die zweite Ableitung (Änderung des Anstiegs) im Intervall xi−1 ≤ x ≤ xi+1 das Vorzeichen nicht wechselt, wird eine der beiden Formeln einen etwas zu großen, die andere einen etwas zu kleinen Wert liefern, so dass das arithmetische Mittel aus beiden Formeln im Allgemeinen einen besseren Näherungswert liefert. Dieser Mittelwert
![]()
wird als zentrale Differenzenformel bezeichnet und kann geometrisch als Anstieg der Sekante vom Punkt i−1 zum Punkt i+1 gedeutet werden. Auf die gleiche Formel kommt man, wenn man durch die Punkte i−1, i und i+1 eine quadratische Parabel legt und deren Anstieg an der Stelle xi berechnet.
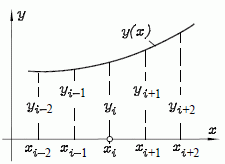
Auf analoge Weise können höhere Ableitungen genähert werden, z. B.:
![]()
wobei in der Klammer die Differenz der ersten Ableitungen an den Zwischenpunkten i+½ und i−½ steht. Nachfolgende Zusammenstellung enthält die Formeln für die ersten vier Ableitungen, in die maximal 5 Punkte einfließen.
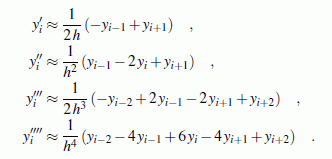
Beispiel
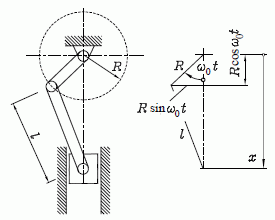
Die skizzierte Schubkurbel wird mit der konstanten Winkelgeschwindigkeit ω0 angetrieben. Bei t = 0 soll die Kurbel ihre tiefste Stelle einnehmen. Gesucht sind die Funktionen x(t) und v(t), die die Lage und die Geschwindigkeit des Kolbens beschreiben.
Gegeben: λ = R/l = 0,4 ; l = 30 cm ; ω0 = 2 s−1 .
Rechts ist eine ausgelenkte Lage mit den wichtigsten Abmessungen skizziert. Die Kurbel hat sich um den Winkel ω0t gedreht.
Die durch die Koordinate x beschriebene Lage des Kolbens ergibt sich aus der Summe der beiden Katheten zweier rechtwinkliger Dreiecke:
![]()
Die Geschwindigkeit des Kolbens v(t) erhält man aus der ersten Ableitung der Funktion x(t) nach der Zeit t. Man erhält nach den Ableitungsregeln mit
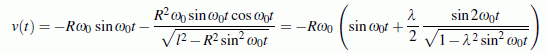
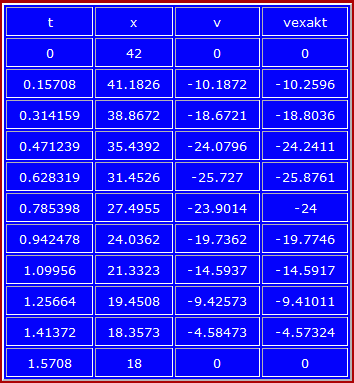
eine Funktion, in der durchaus schon Rechenfehler stecken können. Empfehlenswert ist die Bestätigung dieser Funktion durch numerisches Diefferenzieren von x(t).
Das Programm "Funktionen analysieren" (zu finden unter "TM-interaktiv") realisiert das numerische Differenzieren nach den oben angegebenen Formeln. Rechts sieht man eine Wertetabelle für eine halbe Umdrehung der Kurbel (0 ≤ t ≤ 1,5708 s). Dieser Bereich wurde (sehr grob) in 10 Abschnitte unterteilt, so dass für das numerische Differenzieren h = 0,15708 verwendet wurde. Auf diese Weise wurden die in der Spalte "v" zu sehenden Werte numerisch berechnet. Zum Vergleich sind in der Spalte "vexakt" die Werte zu sehen, die nach der oben analytisch ermittelten Funktion v(t) berechnet wurden. Die Abweichungen sind trotz der groben Schrittweite kleiner als 1%.
Wenn man das numerische Differenzieren dem Computer überträgt, spricht natürlich nichts dagegen, mit wesentlich kleineren Werten für h zu operieren. Eine sehr schöne Kontrolle ergibt sich, wenn man eine analytisch ermittelte Funktionen gemeinsam mit der numerisch berechneten Funktion grafisch darstellt.
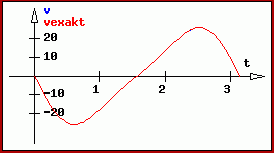
Nebenstehend sieht man die grafische Darstellung der beiden Funktionen "v" (entstanden durch numerisches Differenzieren) und "vexakt" (die analytisch gewonnene Funktion) für eine komplette Kurbelumdrehung. Der Bereich wurde für das numerische Differenzieren in 100 Abschnitte unterteilt.
Man sieht nur eine Kurve, die (blaue) Kurve "v" wird komplett von der roten Kurve "vexakt" überdeckt, ein starkes Indiz für die Richtigkeit der Kurven.

