Eine Strategie für verschiedene Probleme
Folgende Aufgabenstellungen werden betrachtet:
- Für welche Werte der unabhängigen Variablen x ergibt sich der Funktionswert y = f(x) = 0?
- Für welche Werte der unabhängigen Variablen xa, ergibt sich der spezielle Funktionswert f(xa) = a? Diese Frage wird auf die Nullstellen-Berechnung zurückgeführt, indem diese für das modifizierte Problem fa(x) = f(x) − a ausgeführt wird.
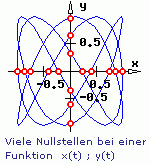Für eine in Parameterdarstellung gegebene Funktion
x = x(t) ; y = y(t)
kann die Forderung "Funktionswert Null" bzw. "Funktionswert vorgeschrieben"
für die beiden Funktionen x(t)
und y(t) erhoben werden.
Jede Berechnung entspricht der Nullstellenberechnung
für
y = f(x).
Unabhängig von der Definition der Funktion reduziert sich das Problem "Nullstellen-Berechnung" auf die Suche nach den (reellen) Werten x, für die y = f(x) = 0 gilt.
Problemanalyse
Zur Nullstellensuche für eine Funktion y = f(x) können folgende allgemeine Aussagen formuliert werden:
- Die geschlossene analytische Lösung der Gleichung f(x) = 0 ist nur in Ausnahmefällen möglich. Hier findet man zwei Beispiele, bei denen dies gelingt.
- Die Fragen,
- wieviel Lösungen und
- ob überhaupt Lösungen im reellen Zahlenbereich existieren,
- "Zeichnen des Funktionsgraphen" (natürlich mit Hilfe geeigneter Software) und/oder
- "Abschätzen", z. B. durch Linearisieren einer nichtlinearen Beziehung, Vergleich mit verwandten Problemen oder auch durch Auswertung "nichtmathematische Informationen" (z. B.: "Nullstelle muss existieren, weil nur so das Gleichgewicht des Systems garantiert werden kann.").
- Im Allgemeinen ist nur eine
numerische Nullstellenberechnung
möglich und zerfällt dabei in zwei
Teilprobleme:
- "Lokalisieren": Suche nach einem Wert x0 in der Nähe der gesuchten Nullstelle bzw. (viel besser!) Angabe eines Bereichs x0 ≤ x ≤ x1 , in dem garantiert eine Nullstelle liegt.
- "Verbesserung der Anfangsnäherung" bis zum Erreichen einer vorgegebenen Genauigkeit.
