Definitionen
Der Grenzwert einer Funktion y = f(x) ist eine Erweiterung des Begriffs "Funktionswert" für den Fall, dass dieser an einer Stelle x0 nicht berechenbar ist (z. B.: "Division durch Null"), aber in beliebiger (unendlich dichter) Nähe von x0 ein endlicher Funktionswert existiert. Man schreibt dann:
![]()
Beispiel 1: Die Funktionswerte x für die Funktion
![]()
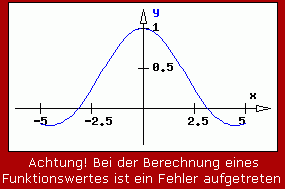
können für beliebige x-Werte außer für x = 0 berechnet werden. Man kann sich leicht überzeugen, dass man für sehr kleine x-Werte Funktionswerte y erhält, die beliebig nahe am Wert 1 liegen. Es lässt sich aber auch problemlos beweisen, dass
![]()
gilt (siehe auch Beispiel 1 auf der Seite "Grenzwerte, Regel von de l'Hospital"). Rechts sieht man die grafische Darstellung der Funktion mit dem Programm "Funktionen analysieren", das man unter "TM-interaktiv" findet. Der Punkt bei x = 0 wird von dem Programm bei der Grafik einfach "übersprungen". Die "Lücke" sieht man wegen der kleinen Schrittweite natürlich nicht, aber eine Ausschrift macht auf die Situation aufmerksam, eine Wertetabelle würde zeigen, welcher Punkt das ist.
Stetigkeit: Eine Funktion y = f(x) heißt an einer Stelle x0 stetig, wenn
- der Funktionswert y(x0) existiert,
- der Grenzwert
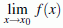 existiert
und
existiert
und 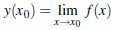 ist.
ist.
Eine Funktion heißt in einem Intervall stetig, wenn sie für alle Punkte des Intervalls stetig ist.
Wenn an einer Stelle kein Funktionswert, aber ein Grenzwert existiert, so spricht man von einer "hebbaren Unstetigkeit". Das oben demonstrierte Beispiel zeigt einen solchen Fall.
Besonderheiten, an Beispielen demonstriert
 Beispiel 2: Die Funktionswerte
x für die Funktion
Beispiel 2: Die Funktionswerte
x für die Funktion
![]()
können für beliebige x-Werte außer für x = 2 berechnet werden. Auch hier gilt, dass für beliebig dichte Annäherung an diesen Punkt endliche Funktionswerte entstehen, allerdings unterschiedliche Werte für Annäherung von links bzw. rechts. Man spricht in diesem Fall vom "linksseitigen bzw. rechtsseitigen Grenzwert" und schreibt:
![]()
Diese Unstetigkeitsstelle gilt als "nicht hebbar".
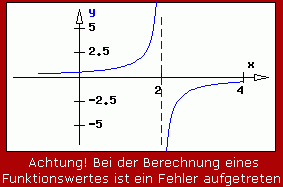 Beispiel 3: Die Funktionswerte
x für die Funktion
Beispiel 3: Die Funktionswerte
x für die Funktion
![]()
können für beliebige x-Werte außer für x = 2 berechnet werden. Hier gilt, dass für beliebig dichte Annäherung an diesen Punkt die Funktionswerte über alle Maßen wachsen. Es ist eine ungerade Polstelle, es gibt keinen endlichen Grenzwert:
![]()
Diese Unstetigkeitsstelle ist natürlich auch "nicht hebbar".
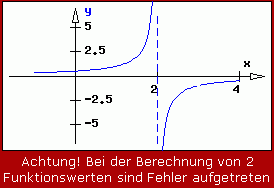 Beispiel 4: Die grafische Darstellung
der Funktion
Beispiel 4: Die grafische Darstellung
der Funktion
![]()
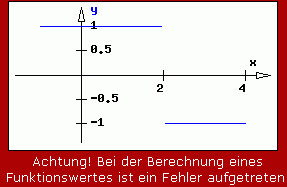
sieht exakt so aus wie die Kurve des Beispiels 3. Allerdings wird vermerkt, dass für 2 Punkte die Funktionswerte nicht berechnet werden konnten. Klarheit schafft die Zerlegung des Nenners der Funktion:
![]()
An der Stelle x = 2 gibt es die gleiche nicht hebbare Unstetigkeit wie beim Beispiel 3. An der Stelle x = 3 ist die Unstetigkeit hebbar: Man könnte den Faktor (3 − x) kürzen, wenn er nicht für x = 3 den Wert Null annehmen würde. Aber in beliebiger Nähe zu diesem Punkt darf man diesen Faktor natürlich kürzen, und es bleibt ein endlicher Funktionswert. Es gilt also:
![]()
Weil für die grafische Darstellung eine recht grobe Schrittweite eingestellt wurde, sieht man sogar die "Lücke" im Kurvenverlauf.
Für die Berechnung der Grenzwerte wurden hier spezielle Überlegungen angestellt. Es gibt allerdings auch eine Strategie, mit der man systematisch vorgehen kann. Diese wird auf der Seite "Grenzwerte, Regel von de l'Hospital" vorgestellt.

