
Wenn eine Kurve in einem kartesischen Koordinatensystem durch eine Funktion y = y(x) beschrieben wird, dann kann der Inhalt der Fläche, die von dieser Funktion, zwei vertikalen Linien bei x = a bzw. x = b und der x-Achse begrenzt wird (Skizze rechts) nach
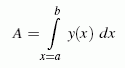
berechnet werden.
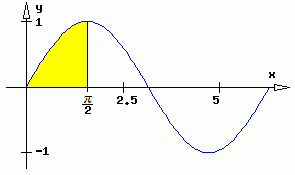
Beispiel: Die Fläche, die vom ersten Viertel einer vollen Schwingung einer Sinuskurve eingeschlossen wird (nebenstehend gelb gezeichnet), führt entsprechend
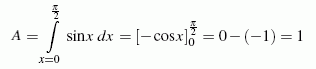
auf ein bemerkenswertes Ergebnis (hier wird deshalb dieses Integral als Test der Genauigkeit der numerischen Integration genutzt).
Man beachte: Das Ergebnis der Integration ist im Allgemeinen vorzeichenbehaftet. Die Integration der Sinuskurve über eine volle Schwingung liefert entsprechend
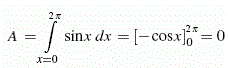
die Summe der positven Fläche unter der ersten Halbwelle und der negativen Fläche der zweiten Halbwelle.
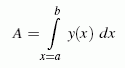
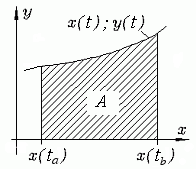
Parameterdarstellung
Wenn die Funktion entsprechend
x = x(t) ; y = y(t)
in Parameterdarstellung gegeben ist, dann wird wegen
![]()
aus der Flächenformel
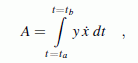
wobei auch die Integrationsgrenzen entsprechend zu transformieren sind.
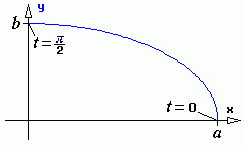
Beispiel: Mit der Parameterdarstellung
x = a cos t , y = b sin t
wird eine Ellipse beschrieben. Es ist die Fläche zu berechnen, die von einem Viertel der Ellipse umschlossen wird (nebenstehende Skizze).
Die beiden Scheitelpunkte der Ellipse liegen bei t = 0 und π/2. Mit der oben angegebenen Formel berechnet man:
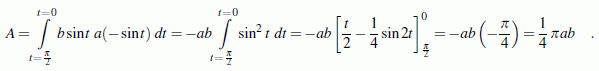
Das Beispiel zeigt, dass schon für relativ einfache Probleme zumindest Grundfertigkeiten in der "Kunst des Integrierens" gefordert sind. Es gibt in der Regel keinen Grund, nicht die oben angegebene Offerte für die numerische Integration zu nutzen.

