Definition des Begriffs "Funktion"
Funktionen dienen dazu, den Zusammenhang von ein oder mehreren Größen (unabhängige Variable) mit einer anderen Größe (abhängige Variable) zu beschreiben. Hier werden zunächst Funktionen behandelt, die nur von einer unabhängigen Variablen abhängig sind (hier findet man eine Einführung in die Darstellung von Funktionen mit zwei unabhängigen Variablen).
Definition: Eine Funktion wird durch eine Vorschrift definiert, die jedem Element x (unabhängige Variable) aus einer Menge D (Definitionsbereich) genau ein Element y (abhängige Variable) aus einer Menge W (Wertebereich) zuordnet, symbolisch dargestellt als y = f(x).
Eine besonders wichtige Rolle beim Arbeiten mit Funktionen spielt ihre Visualisierung als grafische Darstellung ("Graph" einer Funktion, Bemerkung zur Schreibweise). Deshalb wird in der folgenden Übersicht immer auch diese Variante gezeigt.
Beschreibung von Funktionen
| Beispiel | Graph für das Beispiel | |||
| Analytische Darstellung |
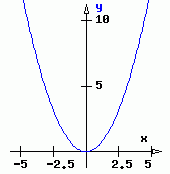
y = f(x) | "Klassische" Darstellung einer Funktion mittels Funktionsgleichung mit der Vorstellung, dass die x-y-Wertepaare in einem kartesischen Koordinatensystem den Funktionsgraphen erzeugen. | Parabel |
 |
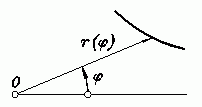
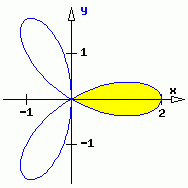
| Darstellung mit Polarkoordinaten | r = r(φ) |
Dies ist auch eine analytische Darstellung mit der Interpretation für φ als Winkel und r als Abstand von einem festen Punkt. |
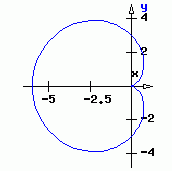 |
|
| Parameter- darstellung (kartesische Koordinaten) |
x = x(t) y = y(t) |
Mit einer unabhängigen Variablen (hier: t) werden mehrere Funktionen (hier: 2) mit analytischen Darstellungen beschrieben, die als kartesische Koordinaten interpretiert werden. Typische Anwendung: Beschreibung von Bewegungen. | 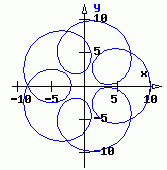 |
|
| Parameter- darstellung (Polarkoordinaten) |
r = r(t) φ = φ(t) |
Mit einer unabhängigen Variablen (hier: t) werden mehrere Funktionen (hier: 2) mit analytischen Darstellungen beschrieben, die als Polarkoordinaten interpretiert werden. Typische Anwendung: Beschreibung von Bewegungen. | 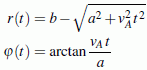 |
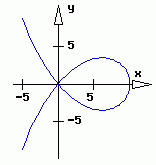 |
| Analytische Darstellung, bereichsweise |
y1 = f1(x1) (x11≤x1≤x12), y2 = f2(x2) (x21≤x2≤x22), ... |
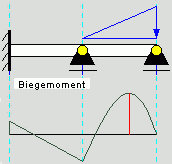
Die Funktionen können mit analytischen Ausdrücken definiert werden, die aber auf bestimmte Bereiche der unabhängigen Variablen beschränkt sind, weil z. B. in einem Bereich eine lineare Abhängigkeit vorliegt und die Definition in einem anderen Bereich eine Funktion höheren Grades (oder auch trigonometrische Funktionen) enthält. Typische Beispiele sind Biegelinien, Biegemoment- und Querkraftverläufe. | 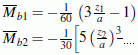 Biegemoment, im linken Abschnitt linear, rechts Funktion 3. Grades |
 |
| Wertetabelle |  |
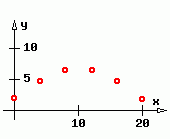
Eine Wertetabelle enthält für diskrete Punkte zu den Werten der unabhängigen Variablen jeweils die Werte der zugehörigen abhängigen Variablen. Dies kann sich auf die Darstellungen y = f(x), r = r(φ) oder die Parameterdarstellung x = x(t) ; y = y(t) beziehen. | 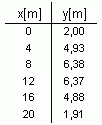 "Kugelstoßen" |
 |
| Funktionensatz | y1 = f1(x) y2 = f2(x,y1) ... y = f(x,y1,...) |
Die Funktion steht am Ende eines Satzes mehrerer Funktionen. Jede Funktion darf die unabhängige Variable und alle vorab definierten Funktionen enthalten. |  System mit "weicher Feder" |
|
| Komplizierter Zusammenhang, nur für einzelne Punkte zu beschreiben | yi = f(xi) | Der Zusammenhang yi = f(xi) wird durch einen komplizierten und/oder sehr aufwendigen Algorithmus (z. B. eine nichtlineare Differenzialgleichung, eine sehr große Determinante) oder ein Experiment beschrieben. |  Stabpendel mit großen Ausschlägen |
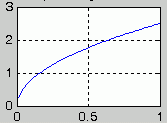 Schwingungsdauer abhängig von Stablänge |
Typische Aufgaben und Fragestellungen
Die Wahl der geeigneten Darstellungsart ist problemabhängig. Deshalb ist z. B. die Umwandlung einer Darstellungsart in eine andere eine typische Aufgabe (siehe z. B.: Kartesische Koordinaten ↔ Parameterdarstellung, Polarkoordinaten → Parameterdarstellung). Besonders wichtig ist die grafische Darstellung, die besonders hilfreich auch bei der Beantwortung folgender Problemstellungen ist:
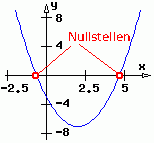 Berechnung der Nullstellen: Für
welche Werte der unabhängigen
Variablen x ergibt sich der
Funktionswert y = 0?
Die Frage kann sich auf den gesamten Definitionsbereich
der unabhängigen Variablen x
beziehen oder auf einen vorgegebenen Bereich. Es können
alle Nullstellen in einem Bereich gefragt sein oder aber
"eine Nullstelle in der Nähe von ...", siehe Seite
"Nullstellen-Berechnung".
Berechnung der Nullstellen: Für
welche Werte der unabhängigen
Variablen x ergibt sich der
Funktionswert y = 0?
Die Frage kann sich auf den gesamten Definitionsbereich
der unabhängigen Variablen x
beziehen oder auf einen vorgegebenen Bereich. Es können
alle Nullstellen in einem Bereich gefragt sein oder aber
"eine Nullstelle in der Nähe von ...", siehe Seite
"Nullstellen-Berechnung".
- Funktionswert soll einen vorgegebenen Wert annehmen:
Die Suche nach dem Wert der unabhängigen Variablen
xa,
für die der
Funktionswert den speziellen Wert
f(xa) = a
annimmt, wird auf die Nullstellen-Berechnung überführt,
indem diese für das modifizierte Problem
fa(x) = f(x) − a
ausgeführt wird, siehe Seite
"Nullstellen-Berechnung".
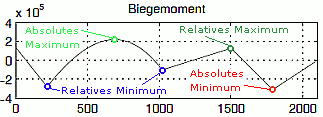 Berechnung relativer und absoluter Extremwerte:
Als relatives Maximum (Minimum) wird ein Funktionswert bezeichnet,
der in seiner unmittelbaren Umgebung den größten (kleinsten)
Funktionswert hat (siehe Seite "Extremwert-Berechnung").
Ein absolutes Maximum (Minimum) in einem
vorgegebenen Bereich ist der Punkt mit dem größten (kleinsten)
Funktionswert. Man beachte den Unterschied zum absolut größten
Funktionswert in einem Bereich, bei dem nur der Betrag des
Funktionswertes (nicht sein Vorzeichen) entscheidend ist.
Berechnung relativer und absoluter Extremwerte:
Als relatives Maximum (Minimum) wird ein Funktionswert bezeichnet,
der in seiner unmittelbaren Umgebung den größten (kleinsten)
Funktionswert hat (siehe Seite "Extremwert-Berechnung").
Ein absolutes Maximum (Minimum) in einem
vorgegebenen Bereich ist der Punkt mit dem größten (kleinsten)
Funktionswert. Man beachte den Unterschied zum absolut größten
Funktionswert in einem Bereich, bei dem nur der Betrag des
Funktionswertes (nicht sein Vorzeichen) entscheidend ist.
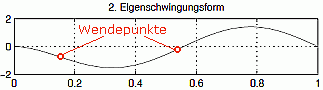 Berechnung des "Änderungsverhaltens":
(größer oder kleiner werdende
Funktionswerte bei Änderung der unabhängigen Variablen), in der
grafischen Darstellung als "Anstieg" zu erkennen (siehe Seite
"Änderungsverhalten, Ableitung, Grenzwert").
An Wendepunkten
wechselt die "Krümmung" des Graphen, der die
Funktion repräsentiert, das Vorzeichen (ein Punkt, der sich entlang des
Graphen bewegt, geht von einer Rechts- in eine Linkskurve über
oder umgekehrt, siehe nebenstehende Animation).
Berechnung des "Änderungsverhaltens":
(größer oder kleiner werdende
Funktionswerte bei Änderung der unabhängigen Variablen), in der
grafischen Darstellung als "Anstieg" zu erkennen (siehe Seite
"Änderungsverhalten, Ableitung, Grenzwert").
An Wendepunkten
wechselt die "Krümmung" des Graphen, der die
Funktion repräsentiert, das Vorzeichen (ein Punkt, der sich entlang des
Graphen bewegt, geht von einer Rechts- in eine Linkskurve über
oder umgekehrt, siehe nebenstehende Animation).
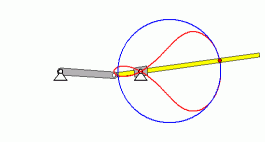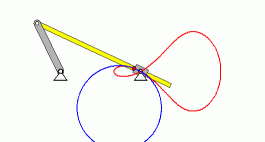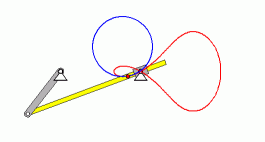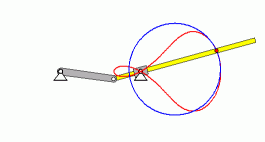 Berechnung der Bogenlänge
der Kurve, die durch die Funktion
repräsentiert wird (siehe Seite
"Bogenlänge einer Kurve").
Für die nebenstehend zu sehende Animation
würde die Fragestellung zum Beispiel lauten: Wie lang ist der
Weg, den der rote Punkt auf der Getriebestange bei einem
Umlauf der Kurbel zurücklegt?
Berechnung der Bogenlänge
der Kurve, die durch die Funktion
repräsentiert wird (siehe Seite
"Bogenlänge einer Kurve").
Für die nebenstehend zu sehende Animation
würde die Fragestellung zum Beispiel lauten: Wie lang ist der
Weg, den der rote Punkt auf der Getriebestange bei einem
Umlauf der Kurbel zurücklegt?
- Berechnung der Krümmung und des Krümmungskreises
für bestimmte
Punkte der Kurve, die durch die Funktion repräsentiert wird
(siehe Seite
"Krümmung, Krümmungsradius, Krümmungskreis").
Für die nebenstehend zu sehende Animation
würde die Fragestellung zum Beispiel lauten: Wie groß sind
die Radien der (blau gezeichneten) Krümmungskreise
für beliebige Punkte der (rot gezeichneten) Bahnkurve. Welche
Koordinaten haben die Mittelpunkte der Krümmungskreise?
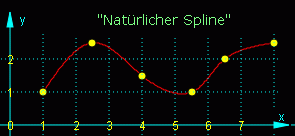 Interpolations- und Ausgleichsrechnung:
Wenn ein Satz von Punkten (Wertetabelle) gegeben ist, gibt es verschiedene
Strategien, daraus (möglichst glatte) Funktionen zu erzeugen. Mit
"natürlichen Splines",
die alle Punkte treffen, gelingt dies. Alternativ dazu
kann mit der "Ausgleichsrechnung" oder mit
"Bézier-Splines" eine
Funktion erzeugt werden, die sich den gegebenen Punkten auf wohl
definierte Art gut annähhern.
Interpolations- und Ausgleichsrechnung:
Wenn ein Satz von Punkten (Wertetabelle) gegeben ist, gibt es verschiedene
Strategien, daraus (möglichst glatte) Funktionen zu erzeugen. Mit
"natürlichen Splines",
die alle Punkte treffen, gelingt dies. Alternativ dazu
kann mit der "Ausgleichsrechnung" oder mit
"Bézier-Splines" eine
Funktion erzeugt werden, die sich den gegebenen Punkten auf wohl
definierte Art gut annähhern.
- Berechnung von Flächen, die durch Kurven begrenzt werden (siehe Seiten "Fläche unter einer Kurve" und "Sektorfläche (Polarkoordinaten)".
![]() Hilfreich bei der Lösung dieser Probleme ist das Programm
"Funktionen analysieren",
das man unter
"TM-interaktiv"
findet (kein Download einer Software erforderlich, Lösungen direkt
im Browser erzeugen).
Hilfreich bei der Lösung dieser Probleme ist das Programm
"Funktionen analysieren",
das man unter
"TM-interaktiv"
findet (kein Download einer Software erforderlich, Lösungen direkt
im Browser erzeugen).