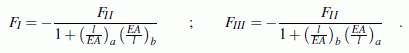Finite-Elemente-Baukasten Femset

Die Rolle der Element-Steifigkeits-Beziehung

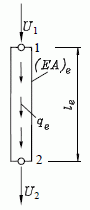
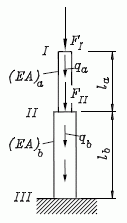
Die besondere Stärke der Finite-Elemente-Methode ist, dass alle an das Ergebnis zu stellenden Forderungen (Berücksichtigung von Materialeigenschaften und Geometrie, Gleichgewicht, Kompatibilität, Randbedingungen) durch formale Prozesse mit Matrizen erfüllt werden. Dies wurde auf den Seiten "Einführungsbeispiel (Element-Steifigkeit, System-Steifigkeit)" an dem einfachsten Element der Elastostatik (Bild links) und auf der Seite "Lösung für die System-Steifigkeitsbeziehung" an dem einfachen Beispiel mit nur zwei Elementen (Bild rechts) demonstriert. Dort wurde die physikalische Begründung für die einzelnen Schritte gegeben.

Hier sollen die einzelnen Schritte noch einmal unter dem wichtigen Aspekt der "Formalisierung" beschrieben werden, um zu verdeutlichen, dass sich die Individualität eines Problems auf einen sehr kleinen Bereich beschränkt, während der weitaus größte Teil der Rechnung für fast alle Problemklassen einem identischen Prozess folgt.

Die Problemklasse, der eine Aufgabe zuzuordnen ist, wird im Wesentlichen durch die Element-Steifigkeitsbeziehung erfasst. Im betrachteten Beispiel ist dies das "Fluchtende Stabelement für elasto-statische Berechnungen", für das die Element-Steifigkeitsbeziehung durch die Element-Steifigkeitsmatrix K_e und den Vektor der reduzierten Elementlasten f_e,red repräsentiert wird:

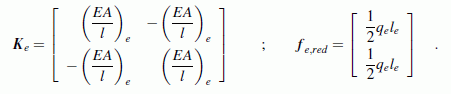
Matrix K_e und Vektor f_e,red müssen als Formel (wie in diesem einfachen Fall) oder als Algorithmus, der den Aufbau beschreibt, bereitgestellt werden. Für eine Reihe von Problemklassen können diese Berechnungs-Vorschriften über die Seite "Elemente verschiedener Problemklassen - Übersicht" erreicht werden. Danach startet der nachfolgend beschriebene formale FEM-Algorithmus.

Der formale FEM-Algorithmus

• Die Informationen über die Materialeigenschaften und die Geometrie (Abmessungen der Elemente) stecken in den Element-Steifigkeitsmatrizen. Elementbelastungen (hier: Eigengewicht) gehen in die Rechnung über die Vektoren der reduzierten Elementlasten ein. Diese werden für einen bestimmten Elementtyp (hier: Fluchtendes Stabelement) nach einem einmal festzulegenden Algorithmus (hier: K_e und f_e,red werden durch die oben angegebenen Formeln definiert) aufgebaut.
• Die Kompatibilität der Verschiebungen der einzelnen Elemente wird über die Knoten erreicht, indem die Verschiebungen der Elementknoten durch die Verschiebungen der System-Knoten ersetzt werden. Die Verschiebungen der Knoten 1 und 2 beider Elemente wurden zu den Knotenverschiebungen der Knoten I, II und III:

  

  Die rechts mit römischen Zahlen dargestellte so genannte Koinzidenzmatrix beschreibt die topologische Zusammensetzung der Struktur aus den Elementen (jede Zeile enthält die Knotennummern eines Elements).
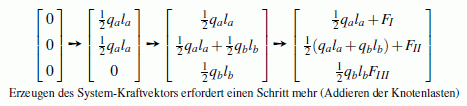
• Gleichgewicht zwischen den inneren Kräften und den äußeren Belastungen wird durch das Einspeichern der Element-Steifigkeitsmatrizen in die System-Steifigkeitsmatrix und das Einspeichern der Vektoren der reduzierten Elementlasten und der Knotenkräfte in den System-Kraftvektor erzielt: In eine Null-Matrix wird zunächst die Element-Steifigkeitsmatrix des Elements a auf die Positionen gespeichert, die durch die Koinzidenzmatrix vorgegebenen werden (betrifft hier die Zeilen bzw. Spalten I und II). Algorithmisch übereinstimmend mit dem Prozess für die nachfolgenden Elemente ist die Interpretation: Die Matrixelemente werden "zu den Null-Elementen addiert".
  
  Danach wird die Element-Steifigkeitsmatrix des Elements b eingefügt, indem alle Matrixelemente auf die wieder durch die Koinzidenzmatrix bestimmten Positionen (hier: Zeilen bzw. Spalten II und III) addiert werden. Für das behandelte Beispiel ist die System-Steifigkeitsmatrix damit komplett:



Entsprechend wird der System-Kraftvektor erzeugt:



• Die verhinderten Verschiebungen (geometrische Randbedingungen) werden eingearbeitet, indem man die zu einer Nullverschiebung (im Beispiel: u_III am Knoten III) gehörenden Zeilen und Spalten der System-Steifigkeitsmatrix und die entsprechenden Positionen im System-Verschiebungsvektor und im System-Kraftvektor streicht:

  

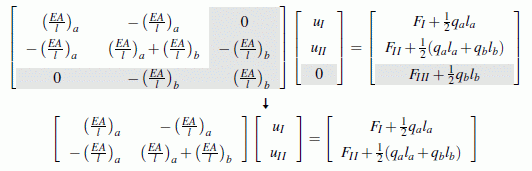
• Die System-Steifigkeitsbeziehung nach Einbau der Randbedingungen ist ein lineares Gleichungssystem, das mit einem einschlägigen Verfahren gelöst werden kann. Man erhält die Knotenverschiebungen. Mit diesen können die beim Einarbeiten der geometrischen Randbedingungen gestrichenen Gleichungen genutzt werden, um die unbekannten Kräfte (Lagerreaktionen) zu berechnen.

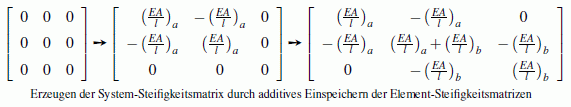
Modifizierte Systeme

Neben dem oben beschriebenen hohen Formalisierungsgrad des Finite-Elemente-Algorithmus, der der Programmierung außerordentlich entgegenkommt (Erfüllung der Gleichgewichtsbedingungen durch "Einspeichern", Berücksichtigung der Lagerung durch "Zeilen-Spalten-Streichen"), ist die Möglichkeit der einfachen Variation der berechneten Struktur ein gewaltiger Vorteil:

• Eine Änderung der Belastung (oder ein zusätzlicher Lastfall) beeinflusst die System-Steifigkeitsmatrix nicht. Wenn für die Lösung des Gleichungssystems ein geeignetes Eliminationsverfahren benutzt wird, braucht die Dreieckszerlegung der Koeffizientenmatrix (im Allgemeinen der aufwendigste Teil der Finite-Elemente-Berechnung überhaupt) in diesem Fall nicht neu ausgeführt zu werden.
• Änderungen der Element-Abmessungen und der Materialeigenschaften können berücksichtigt werden, indem einzelne Elemente aus der System-Steifigkeitsmatrix wieder entfernt (Einspeichern "negativer" Elemente) und neue Elemente hinzugefügt werden (Berechnung verschiedener Varianten einer Konstruktion).
• Nach dem Aufbau der System-Steifigkeitsmatrix kann diese durch unterschiedliche Lagerung der Struktur unterschiedlich modifiziert werden (Berechnung verschiedener Lagerungsvarianten einer Konstruktion).
• Die statisch unbestimmte Lagerung eines Systems macht die Berechnung weder komplizierter noch aufwendiger, im Gegenteil: Das nachfolgende Beispiel zeigt, dass sich die Anzahl der Gleichungen im linearen Gleichungssystem sogar verringert.

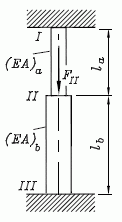
Beispiel: Das links zu sehende System diente auf der Seite "Einführungsbeispiel (Element-Steifigkeit, System-Steifigkeit)" als Demonstrationsbeispiel für das Formulieren der System-Steifigkeits-Beziehung. Der nebenstehend rechts skizzierte Stab hat die gleichen Abmessungen und Materialeigenschaften. Er trägt jedoch nur eine äußere Kraft F_II und ist an den Punkten I und III (statisch unbestimmt) gelagert (auch das Eigengewicht soll unberücksichtigt bleiben, würde jedoch die Aufgabe nicht nennenswert komplizierter machen).

Die für das links dargestellte System aufgebaute System-Steifigkeitsbeziehung kann wieder verwendet werden (unter Verzicht auf q_a und q_b im System-Kraftvektor), weil sich die Abmessungen und Materialeigenschaften nicht geändert haben. Die beiden geometrischen Randbedingungen

u_I = 0   und   u_III

werden durch Streichen der ersten und dritten Zeile (Spalte) realisiert, und das Gleichungssystem degeneriert zu einer einzigen Gleichung,

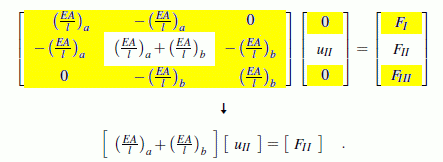
Die Lösung liefert die Verschiebung des Punktes II:

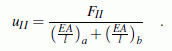
Mit diesem Ergebnis ergeben sich die Kräfte bei I und III (Lagerreaktionen) auch hier aus den (zunächst gestrichenen) Gleichungen 1 und 3 der System-Steifigkeitsbeziehung: