Für ausgewählte Problemklassen werden hier die Grundlagen für das Erzeugen von
Element-Steifigkeitsbeziehungen beschrieben. In der folgenden Zusammenstellung
findet man die Links zur Behandlung der einzelnen Elementtypen.
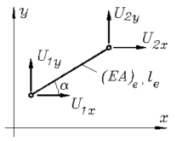
Ebenes Fachwerk-Element
(Truss2D, Schlüssel: 10)
|
kx = 2
kf = 2
ke = 2
kp = 1
|
Weil mit den Knotenkoordinaten auch die Elementlänge
le und der Winkel
α bekannt sind, wird nur
ein Elementparameter benötigt: Dehnsteifigkeit
EA.
Theoretische Grundlagen: "Dankert/Dankert: Technische Mechanik", Kapitel
"Der Stab als finites Element".
|
|
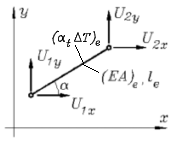
Ebenes Fachwerk-Element mit Temperaturdehnung
(Truss2DT, Schlüssel: 11)
|
kx = 2
kf = 2
ke = 2
kp = 2
|
Weil mit den Knotenkoordinaten auch die Elementlänge
le und der Winkel
α bekannt sind, werden nur
zwei Elementparameter benötigt: Dehnsteifigkeit
EA und das Produkt
αt ΔT aus
dem Temperaturausdehnungskoeffizienten und der
Temperaturerhöhung.
Theoretische Grundlagen: "Dankert/Dankert: Technische Mechanik", Kapitel
"Der Stab als finites Element".
|
|
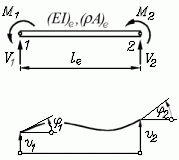
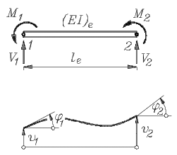
Ebenes biegesteifes Element
(Bend2D, Schlüssel: 15)
|
kx = 1
kf = 2
ke = 2
kp = 3
|
Weil mit den Knotenkoordinaten auch die Elementlänge
le bekannt ist, werden nur
drei Elementparameter benötigt: Biegesteifigkeit
EI und die Intensitäten
der Linienlast an den beiden Elementknoten
q1 und
q2.
Theoretische Grundlagen: "Dankert/Dankert: Technische Mechanik", Kapitel
"Computerverfahren für Biegeprobleme".
|
|
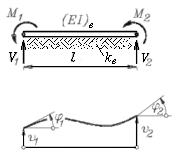
Ebenes biegesteifes Element mit elastischer Bettung
(Bd2DeB, Schlüssel: 17)
|
kx = 1
kf = 2
ke = 2
kp = 4
|
Weil mit den Knotenkoordinaten auch die Elementlänge
le bekannt ist, werden nur
vier Elementparameter benötigt: Biegesteifigkeit
EI, Bettungszahl
k und die Intensitäten
der Linienlast an den beiden Elementknoten
q1 und
q2.
Theoretische Grundlagen: "Dankert/Dankert: Technische Mechanik", Kapitel
"Spezielle Biegeprobleme".
|
|
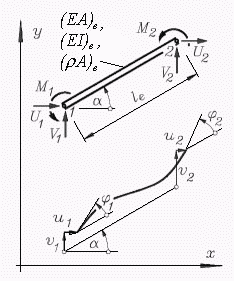
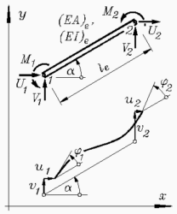
Ebenes biege- und dehnsteifes Rahmen-Element
(Beam2D, Schlüssel: 20)
|
kx = 2
kf = 3
ke = 2
kp = 4
|
Weil mit den Knotenkoordinaten auch die Elementlänge
le und der Winkel
α bekannt sind, werden nur
vier Elementparameter benötigt: Biegesteifigkeit
EI, Dehnsteifigkeit
EA und die Intensitäten
der Linienlast an den beiden Elementknoten
q1 und
q2.
Theoretische Grundlagen: "Dankert/Dankert: Technische Mechanik", Kapitel
"Computerverfahren für Biegeprobleme".
|
|
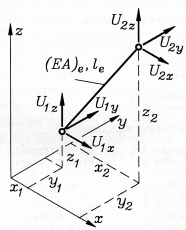
Räumliches Fachwerk-Element
(Truss3D, Schlüssel: 110)
|
kx = 3
kf = 3
ke = 2
kp = 1
|
Weil alle geometrischen Größen aus den Knotenkoordinaten berechnet werden können,
wird nur
ein Elementparameter benötigt: Dehnsteifigkeit
EA.
|
|
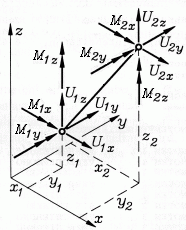
Räumliches biege-, dehn- und torsionssteifes Element
(Beam3D, Schlüssel: 120)
|
kx = 3
kf = 6
ke = 2
kp = 6
|
Weil alle geometrischen Größen aus den Knotenkoordinaten berechnet werden können,
werden nur
sechs Elementparameter benötigt: Elastizitätsmodul
E, Gleitmodul
G, Flächenträgheitsmomente
I xx und
I yy (bezogen auf
Hauptzentralachsen), Torsionsträgheitsmoment
It und Querschnittsfläche
A.
Die lokale Koordinate y, auf
die sich ein Hauptträgheitsmoment bezieht, muss parallel zur
x-y-Ebene liegen.
|
|
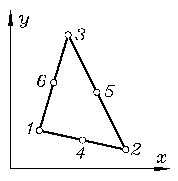
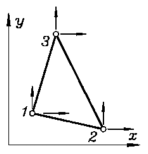
Ebenes Drei-Knoten-Scheiben-Element SD6
(Plane3_6, Schlüssel: 1036)
|
kx = 2
kf = 2
ke = 3
kp = 3
|
Weil mit den Knotenkoordinaten die Abmessungen in der Ebene bekannt sind, werden nur
drei Elementparameter benötigt: Elementdicke
t, Elastizitätsmodul
E und
Querkontraktionszahl ν.
Theoretische Grundlagen: "Dankert/Dankert: Technische Mechanik", Kapitel
"Methode der finiten Elemente".
|
|
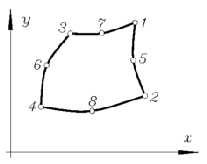
Ebenes Acht-Knoten-Scheiben-Element SV16
(Plane4_16, Schlüssel: 1416)
|
kx = 2
kf = 2
ke = 8
kp = 3
|
Weil mit den Knotenkoordinaten die Abmessungen in der Ebene bekannt sind, werden nur
drei Elementparameter benötigt: Elementdicke
t, Elastizitätsmodul
E und
Querkontraktionszahl ν.
Theoretische Grundlagen: "J. Dankert: Numerische Methoden der Mechanik", Kapitel
"Die Methode der finiten Elemente".
|
|