Grundgleichungen der Finite-Elemente-Methode

Während beim "klassischen" Ritz-Verfahren die Ansatzfunktionen für das gesamte Gebiet des zu untersuchenden Bauteils formuliert werden, wird bei der Finite-Elemente-Methode jeweils ein Ritz-Ansatz für die Verschiebungen eines Teilgebiets (finites Element) formuliert. Dabei ergibt sich das Problem, dass die Verschiebungen an den Grenzen der Elemente natürlich mit denen der Nachbarelemente kompatibel sein müssen.

Dies wird mit einem besonders eleganten "Trick" erreicht: Als Freiwerte des Verschiebungsansatzes (beim klassischen Ritz-Verfahren die a_i) werden die Verschiebungen an den Knoten, an denen benachbarte Elemente Kontakt haben, verwendet. Dann ist an diesen Knoten automatisch die Kompatibilität der Verschiebungen benachbarter Elemente gesichert. Man muss allerdings darauf achten, dass die Ansatzfunktionen so beschaffen sind, dass die Verschiebungskompatibilität an den Knoten automatisch die Kompatibilität an der gesamten Grenzfläche benachbarter Elemente sicherstellt.

Betrachtet wird der allgemeine zwei- oder dreidimensionale elastische Körper, für den das Prinzip vom Minimum des elastischen Potentials so formuliert werden kann:

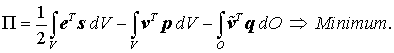
Darin ist e der Vektor der Verzerrungen (Dehnungen und Gleitungen), s der Vektor der Spannungen (Normal- und Schubspannungen), v ist der Vektor der Verschiebungen, p der Vektor der volumenbezogenen Belastung (z. B.: Eigengewicht, Fliehkraft), q der Vektor der Oberflächenlasten (z. B.: Druck).

Zunächst wird nur ein finites Element betrachtet. Es soll n_k Knoten haben, die Knoten haben k_f Knotenfreiheitsgrade (Verschiebungskomponenten, k_f braucht nicht für alle Knoten gleich zu sein), insgesamt möge das Element n_f Freiheitsgrade haben. Für das Element ist nun ein Ansatz für das Verschiebungsfeld in der Form

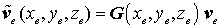
erforderlich ist (bezogen auf ein elementeigenes Koordinatensystem). In v_e sind alle n_f Verschiebungen an allen Knoten des Elements zusammengefasst (Elementverschiebungsvektor), und weil das Verschiebungsfeld für alle Punkte des Elements (auch für die Knoten) gilt, muss die Matrix der Ansatzfunktionen G so beschaffen sein, dass beim Einsetzen der Koordinaten eines Knotens das Produkt Gv_e den entsprechenden Knotenverschiebungsvektor ergibt.

Gelingt es nicht, eine solche Matrix aufzuschreiben, so kann zunächst ein Verschiebungsansatz

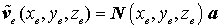
mit allgemeinen Freiwerten a_i gewählt werden (die Anzahl der Freiwerte und damit die Anzahl der Spalten von N müssen mit der Anzahl der Freiheitsgrade n_f des Elements übereinstimmen). Der Elementverschiebungsvektor kann nun durch Einsetzen der Koordinaten der einzelnen Knoten folgendermaßen aufgeschrieben werden:

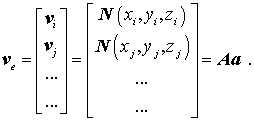
Die Matrix A enthält ausschließlich Knotenkoordinaten. Mit ihrer Inversen können die allgemeinen Ansatzparameter entsprechend

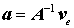
durch die Knotenverschiebungen ersetzt werden. Damit kann der allgemeine Ansatz in der Form

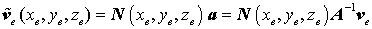
geschrieben werden, und daraus liest man die Matrix der Ansatzfunktionen

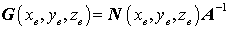
ab, die die eingangs gestellte Forderung nach der Verknüpfung der Elementknotenverschiebungen mit dem Verschiebungsfeld im Inneren des Elements

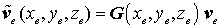
erfüllt.

Die elastischen Verzerrungen e in der Formel des elastischen Potentials sind mit den Verschiebungen durch eine Beziehung

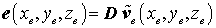
verknüpft. Hierin ist D ein Matrixdifferenzialoperator. Einsetzen des Verschiebungsansatzes ergibt:

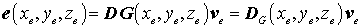
mit

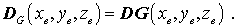
Die Spannungen s in der Formel des elastischen Potentials sind mit elastischen Verzerrungen über ein Stoffgesetz (z. B. das Hookesche Gesetz) verknüpft:

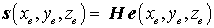
(an die Stelle der Spannungen können auch Schnittgrößen treten - Kirschoffsche Plattentheorie, Bernoullische Biegetheorie, ... -, dann repräsentiert H deren Zusammenhang mit den Krümmungen).

Mit

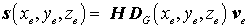
kann der Anteil eines einzelnen finiten Elements am elastischen Potential so formuliert werden (man beachte, dass sich beim Transponieren eines Produkts die Reihenfolge der Faktoren umkehrt):

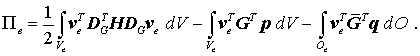
Die Knotenverschiebungsvektoren können aus den Integralen herausgezogen werden, für die verbleibenden Integrale werden sinnvolle Abkürzungen eingeführt:

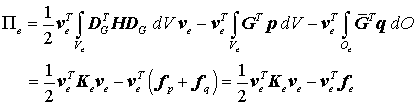
mit der sogenannten Elementsteifigkeitsmatrix

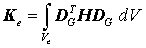
und dem Elementbelastungsvektor infolge der Volumen- und Oberflächenlasten

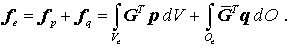
Das gesamte elastische Potential ergibt sich aus der Summierung der Potentiale aller Elemente:

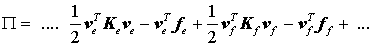
(hier nur angedeutet mit den beiden Elementen e und f).

Zur Erinnerung: Dies ist (nach einer etwas aufwändigen Zwischenrechnung) das Gesamtpotential, aufgeschrieben mit Ritzschen Ansatzfunktionen. Diese sind über die Integralausdrücke in die Elementsteifigkeitsmatrizen und die Elementbelastungsvektoren eingeflossen, während die Ritzschen Ansatzparamter als Knotenverschiebungen (z. B. in v_e und v_f) in separaten Vektoren konzentriert sind.

Die Ansatzparameter (Knotenverschiebungen) werden nun nach der Vorschrift von Ritz durch das Nullsetzen der partiellen Ableitungen des Gesamtpotentials nach den Ansatzparametern bestimmt. Dies kann als Ableitung nach dem Vektor v, in dem alle Knotenverschiebungen aller Knoten des Gesamtsystems enthalten sind, so formuliert werden (hier findet man die Ableitungsregeln für diese Matrix-Vektor-Produkte):

Dies ist ein großes lineares Gleichungssystem

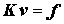
mit der so genannten Systemsteifigkeitsmatrix K und dem Systembelastungsvektor f (eventuell an den Knoten angreifende äußere diskrete Lasten dürfen auf die entsprechenden Positionen in f einfach aufaddiert werden).

Dabei kann in doppelter Hinsicht ausgenutzt werden werden, dass bei der partiellen Ableitung nach einer Knotenverschiebung nur wenige Elemente betroffen sind (genau die, die an diesem Knoten angeschlossen sind). Einerseits führt dies auf eine nur dünn mit von Null verschiedenen Elementen besetzte Koeffizientenmatrix des großen Gleichungssystems, was bei der Lösung mit Vorteil genutzt werden kann. Andererseits bietet es sich an, zunächst nur zu untersuchen, welchen Anteil eine Elementsteifigkeitsbeziehung bei der Ableitung nach den Knotenverschiebungen der eigenen Knoten liefert, um dann danach die Anteile der anderen Elemente zu addieren.

Die Ableitung des Gesamtpotentials nach den in v_e zusammengefassten Knotenverschiebungen des Elementse entsprechend

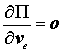
liefert die so genannte Elementsteifigkeitsbeziehung

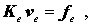
die aus der oben genannten Systemsteifigkeitsbeziehung nur jeweils einen Anteil zu einigen Gleichungen liefert. Alle Elementsteifigkeitsmatrizen zusammen ergeben die Systemsteifigkeitsbeziehung, wenn die Anteile, die in K bzw. f auf die gleichen Positionen fallen, addiert werden. Diese "Einspeicherungsstrategie" entspricht genau dem Algorithmus, der im Kapitel "Der Stab als finites Element" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" am einfachen Beispiel anschaulich hergeleitet wird.

Es ist sinnvoll, den Weg bis zur Systemsteifigkeitsbeziehung zunächst formal so zu gehen, wie es hier beschrieben wurde. Es muss deshalb vermerkt werden, dass der Vorteil, für alle Elemente die gleichen Ansatzfunktionen zu verwenden, mit einem Verstoß gegen die Regeln des Ritzschen Verfahrens erkauft wurde, denn zulässige Vergleichsfunktionen müssen die geometrischen Randbedingungen erfüllen. Das ist zumindest für die Knoten nicht eingehalten worden, die durch starre Lager gebunden sind.

Aber dieser eindeutige Regelverstoß kann nachträglich geheilt werden, weil die Ansatzparameter ja die in der Systemsteifigkeitsbeziehung noch sichtbaren Knotenverschiebungen sind. Wenn in

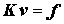
nachträglich alle verhinderten Verschiebungen Null gesetzt werden, dann ist das gleichwertig mit dem nach Ritz korrekten Vorgehen, weil damit genau die Ansatzfunktionen, die mit diesen Ansatzparametern verknüpft waren, ihren Einfluss auf das Ergebnis verlieren.

Das Nullsetzen bestimmter Verschiebungen in der Systemsteifigkeitsbeziehung sollte in jedem Fall so realisiert werden, dass die Symmetrie der Matrix K erhalten bleibt. Dies kann z. B. durch das auf der Seite "FEM-Algorithmus: Beispiel Biegeträger" demonstrierte "Zeilen-Spalten-Streichen" erreicht werden. Die dabei herausgenommenen Gleichungen enthalten auf der rechten Seite eine Unbekannte in f (Lagerreaktion), die nach Berechnung aller Verschiebungen mit Hilfe dieser Gleichung berechnet werden kann.

Es soll noch angemerkt werden, dass vor dem Einarbeiten der verhinderten Verschiebungen das Gleichungssystem ohnehin nicht gelöst werden kann, weil die Systemsteifigkeitsmatrix singulär ist.

Für Biegeträger kann der Unterschied zwischen "klassischem" Ritz-Verfahren und der Finite-Elemente-Methode besonders anschaulich gezeigt werden:

Beim "klassischen" Ritz-Verfahren werden Ansatzfunktionen verwendet, die für die gesamte Länge des Trägers gelten, bei der Finite-Elemente-Methode wird zunächst das Element e betrachtet. In einem elementeigenen Koordinatensystem (Koordinate z_e) werden die Ansatzfunktionen für dieses Element aufgeschrieben. Das Element für den geraden Biegeträger soll 2 Knoten mit je zwei Freiheitsgraden haben (Vertikalverschiebung und Biegewinkel). Hier wird also ein Ansatz in der Form

mit vier Ansatzfunktionen benötigt, die beim Einsetzen der Knotenkoordinaten z_e = 0 (Knoten i) bzw. z_e = l_e (Knoten j) die zugehörige Knotenverformung liefern (das bedeutet z. B., dass g₁(0) = 1 und g₂(0) = g₃(0) = g₄(0) = 0 liefern müssen). Man beachte, dass dies gleichzeitig die Ansatzfunktionen für den Biegewinkel sind, denn es gilt natürlich

Hier soll demonstriert werden, wie man mit einem allgemeinen Ansatz zu den Ansatzfunktionen g kommt (Matrizen im links beschriebenen allgemeinen Fall, die für den Biegeträger zu Vektoren degenerieren, werden hier mit Kleinbuchstaben bezeichnet). In

bzw.

müssen entsprechend den 4 Freiheitsgraden des Elements sowohl vier Ansatzfunktionen als auch vier Freiwerte enthalten sein. Nun wird der Elementverschiebungsvektor durch Einsetzen der Knotenkoordinaten in den allgemeinen Ansatz erzeugt:

Für diesen einfachen Fall kann die Matrix A (mit erträglicher Mühe) "von Hand" invertiert werden, und man kann aus

den Vektor der Ansatzfunktionen berechnen:

mit

Die Analogie zu den nebenstehend beschriebenen allgemeinen Gleichungen soll möglichst deutlich bleiben. Dort gibt es im elastischen Potential den Anteil

Der erste Summand im elastischen Potential für den Biegeträger wird dieser Schreibweise angepasst:

Der Matrix H entspricht hier die Biegesteifigkeit EI, und dem Vektor e entspricht hier die zweite Ableitung der Verschiebung. Der Differentialoperator D wird also besonders einfach, es ist die 2. Ableitung nach der Koordinate z_e:

Die Matrix D_G degeneriert in diesem einfachen Fall zu einem Vektor d_G, der sich nach der Formel

berechnen lässt:

Nun wird der Anteil eines einzelnen Elements am elastischen Potential durch Einsetzen von

formuliert:

Die Knotenverschiebungsvektoren können aus den Integralen herausgezogen werden:

mit der Elementsteifigkeitsmatrix K_e und dem Elementbelastungsvektor f_e:

Das gesamte elastische Potential ergibt sich aus der Summe aller Elementanteile (hier nur mit den beiden Nachbarelementen e und f angedeutet):

Die Ansatzparameter (Knotenverschiebungen) werden nun nach der Vorschrift von Ritz durch das Nullsetzen der partiellen Ableitungen des Gesamtpotentials nach allen Ansatzparametern (Knotenverschiebungen) v₁, φ₁, v₂, φ₂, ... , v_i, φ_i,  v_j, φ_j, ...  bestimmt, was als

formuliert werden kann (v ist der Vektor mit allen Knotenverschiebungen). Die Ableitungen liefern ein lineares Gleichungssystem

mit der Systemsteifigkeitsmatrix K und dem Systembelastungsvektor f (eventuell an den Knoten angreifende äußere diskrete Lasten dürfen auf die entsprechenden Positionen in f einfach aufaddiert werden).

Für den geraden Biegeträger wird besonders deutlich, dass bei den Ableitungen immer nur wenige Elemente betroffen sind. Für die partiellen Ableitungen nach v_j und φ_j z. B. sind es nur die in der Formel des Gesamtpotentials angedeuteten vier Anteile der beiden Elemente e und f, weil nur diese beiden Elemente Kontakt zum Knoten j haben und demzufolge v_j und φ_j nur in den Elementverschiebungsvektoren v_e und v_f vorkommen.

Es ist also sinnvoll, zunächst nur die Ableitung des Gesamtpotentials nach einem Elementverschiebungsvektor v_e auszuführen, um so die Anteile zu bestimmen, den dieses Element zu den Gleichungen für die Knoten i und j liefert und später dann die Anteile der Nachbarelemente hinzuzufügen Aus

erhält man die Elementsteifigkeitsbeziehung

Nach den oben angegebenen Integralformeln können K_e und f_e für diesen einfachen Fall in geschlossener Form angegeben werden (Einsetzen der beiden Vektoren d_G und g und Ausmultiplizieren):

mit   

und   

Für den Sonderfall "Konstante Biegesteifigkeit EI" können die Integrale der k_mn-Formel sogar allgemein gelöst werden, für k₁₂ erhält man z. B.:

Für vorgegebene Funktionen der Linienlast q kann man auch die Integrale der f_m-Formel lösen, z. B. für linear veränderliches q mit der Intensität q_i am Knoten i und q_j am Knoten j. Gemeinsam mit konstanter Biegesteifigkeit ergibt sich dann die Elementsteifigkeitsbeziehung, die im Kapitel "Computer-Verfahren für Biegeprobleme" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" als "Erweiterte Elementsteifigkeitsbeziehung für den ebenen Biegeträger" auf anderem Wege hergeleitet wurde:

Man beachte, dass im Elementbelastungsvektor auf den Positionen 1 und 3 Kräfte und auf den Positionen 2 und 4 Momente stehen.