Das Beispiel
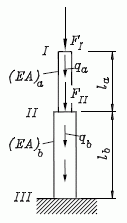
Der skizzierte Stab ist an den Punkten I und II durch die Kräfte FI bzw. FII und zusätzlich durch das Eigengewicht (repräsentiert durch qa und qb) belastet und bei III gelagert.
Gegeben: Ea ; Aa ; la ; qa ; Eb ; Ab ; lb ; qb ; FI ; FII .
Berechnet werden sollen die Verschiebungen der Punkte I und II und die Lagerkraft bei III.
Für dieses kleine Beispiel wird auf der Seite "Einführungsbeispiel (Element-Steifigkeitsbeziehung, System-Steifigkeitsbeziehung)" ausführlich beschrieben, wie nach dem klassischen Finite-Elemente-Algorithmus die so genannte Systemsteifigkeitsbeziehung entsteht, die die gegebenen Belasungen (qa, qb, FI, FII) mit den unbekannten Verschiebungen an den Punkten I und II und der unbekannten Lagerreaktion FIII verknüpft:
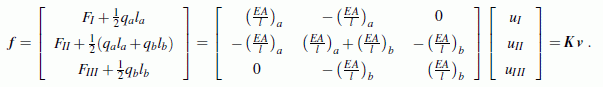
Die System-Steifigkeitsmatrix K ist ...
- ... symmetrisch (bezüglich der Hauptdiagonalen), diese Eigenschaft (beruhend auf dem Satz von Maxwell-Betti) teilt sie mit den Element-Steifigkeitsmatrizen,
- ... im Allgemeinen nur spärlich mit von Null verschiedenen Elementen besetzt, hat häufig eine ausgeprägte Bandstruktur (nur in einem schmalen Band rechts und links von der Hauptdiagonalen sind von Null verschiedene Elemente zu finden), was sich bei diesem einfachen Beispiel durch die Nullen auf den Positionen k13 und k31 schon andeutet,
- ... singulär (kann also nicht invertiert werden, siehe zum Beispiel: "Inverse Transformation").
Die letztgenannte Eigenschaft ist kein Nachteil, denn das Gleichungssystem, das mit der System-Steifigkeitsbeziehung beschrieben wird, enthält ja noch nicht die komplette Information über das zu berechnende System (es ist bisher unberücksichtigt, dass das System am Punkt III gelagert ist).
Um die für die Lösung großer linearer Gleichungssysteme extrem wichtige Symmetrie der Koeffizientenmatrix zu erhalten, wird folgende Strategie praktiziert:
- Die dritte Gleichung (mit der unbekannten Kraft FIII)
wird aus dem Gleichungssystem herausgenommen, gleichzeitig wird die dritte Spalte der
Koeffizientenmatrix K entfernt. Dies ist erlaubt,
weil die Verschiebung uIII gleich Null ist
(Einarbeitung der bisher unberücksichtigten geometrischen Randbedingung).
Das verbleibende reduzierte Gleichungssystem
hat eine reguläre Koeffizientenmatrix (im Gegensatz zur singulären System-Steifigkeitsmatrix K) und kann nach den unbekannten Verschiebungen aufgelöst werden. Man erhält: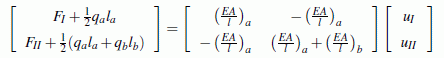
Es ist das erwartete Ergebnis (uI ist die Summe der Längenänderungen beider Stababschnitte, uII entspricht der Längenänderung des Elements b).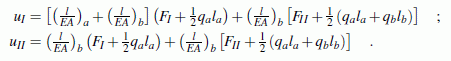
- Die zunächst aus der System-Steifigkeitsbeziehung herausgenommene dritte Gleichung wird
nun bei bekannten Verschiebungen zur Berechnung der noch unbekannten Lagerkraft
FIII verwendet. Mit dem berechneten Wert
von uII und
uIII = 0 ergibt sich:
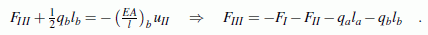
Die besondere Stärke der Finite-Elemente-Methode ist, dass alle an das Ergebnis zu stellenden Forderungen (Berücksichtigung von Materialeigenschaften und Geometrie, Gleichgewicht, Kompatibilität, Randbedingungen) durch formale Prozesse mit Matrizen erfüllt werden.
An dem hier behandelten einfachen Beispiel wurden alle wesentlichen Schritte des Finite-Elemente-Algorithmus sichtbar. Alle physikalischen Zusammenhänge in der Struktur werden durch Einspeichern und Umspeichern der in Matrizen und Vektoren enthaltenen Informationen berücksichtigt.
Auf der Seite "Finite-Elemente-Methode - ein sehr formaler Prozess" werden die physikalischen Zusammenhänge mit den formalen Matrix-Operationen noch einmal detailliert beschrieben.

