|
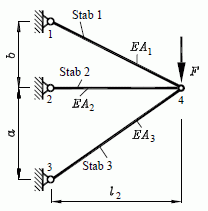
| Beispiel: Zusätzlich zur Kraft F wird das Fachwerk durch Erwärmung eines Stabs belastet |
Element-Belastungsvektor
Fachwerke bestehen aus Stäben, die untereinander über Knoten (theoretisch reibungsfreie Gelenke) verbunden sind. Äußere Kräfte werden nur über die Knoten eingeleitet, so dass die Stäbe nur Druck- oder Zugkräfte ("Stabkräfte") aufnehmen. Dies gilt auch, wenn zusätzlich ein oder mehrere Stäbe durch Temperaturveränderung Stabkräfte erzeugen. Temperaturänderung erzeugen allerdings nur Spannungen (bzw. Stabkräfte) bei statisch unbestimmten Systemen (nebenstehendes Beispiel).
Der einzelne Fachwerkstab verformt sich durch seine Stabkraft und die Temperaturänderung, die (elastische und thermische) Dehnungen (und dadurch eine Längenänderung) des Stabes hervorrufen. Die Längenänderungen aller Stäbe, die dabei selbstverständlich ihre ursprünglich gerade Form beibehalten, führen zu Knotenverschiebungen, die am Knoten i durch zwei Komponenten uix und uiy beschrieben werden (jeder Knoten hat 2 Freiheitsgrade).
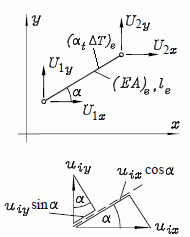
An den Knoten, an denen in der Regel mehr als zwei Stäbe zusammenstoßen, wirken natürlich nicht nur Kräfte in Stablängsrichtung (wie in den Stäben). Deshalb wird als allgemeines (ebenes) Fachwerk-Element ein Stab definiert, der eine beliebige Lage in der Ebene einnimmt, zur x-Achse um den Winkel α gedreht ist und an jedem Knoten zwei Knotenkräfte Uix und Uiy (i = 1 , 2) übertragen kann (nebenstehende Abbildung links). Diese beiden Kraftkomponenten eines Knoten sind natürlich nicht unabhängig voneinander, weil ihre Resultierende Ui in die Stablängsrichtung fallen muss. Es gilt:
![]()
Von den beiden in gleicher Weise wie die Knotenkräfte definierten Knotenverschiebungen uix und uiy (i = 1 , 2) sind jeweils nur die in Stablängsrichtung fallenden Komponenten für die Längenänderung des Stabes verantwortlich. Für die Knotenverschiebung in Stablängsrichtung ui liest man ab:
![]()
Der Zusammenhang zwischen der Verlängerung des Stabes in Stablängsrichtung Δle = (u2 − u1) bzw. der Dehnung des Stabs εe = Δle/le und der Stabkraft U2 ist für linear-elastisches Material durch das erweiterte Hookesche Gesetz εe = σe /Ee + (αt ΔT)e gegeben. Mit σe = U2/Ae kann daraus die folgende Beziehung für U2 aufgeschrieben werden, in der das Produkt aus Elastizitätsmodul und Querschnittsfläche die so genannte "Dehnsteifigkeit" EAe ist. Aus
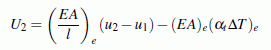
wird durch Ersetzen der Verschiebungen u1 und u2 durch die Verschiebungskomponenten:
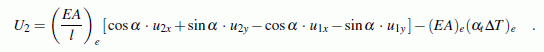
Multiplikation dieser Gleichung mit cos α liefert die Knotenkraftkomponente U2x:
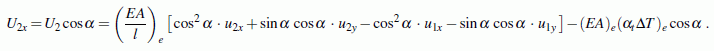
Entsprechend erhält man durch Multiplikation mit sin α die Knotenkraftkomponente U2y. Da
![]()
(Gleichgewicht am Element) gelten muss, sind alle Beziehungen bekannt, die die vier Element-Knotenkräfte mit den vier Element-Knotenverschiebungen verknüpfen. Sie bilden die
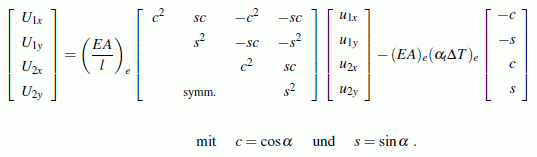
Die Elementsteifigkeitsmatrix ist identisch mit der Matrix für das Stabelement ohne Temperaturbelastung. Diese werden nur als so genannte "reduzierte Elementbelastungen" zusätzlich zu den äußeren Lasten auf die Knoten aufgebracht.
Beispiel

Das skizzierte System ist durch eine Kraft F belastet, und der Stab 2 wird um die Temperaturdifferenz ΔT erwärmt. Für den Stab 2 soll die Elementsteifigkeitsbeziehung berechnet werden.
Gegeben:
a = 320 mm ; αt = 1,2·10−5 K−1 ; EA2 = 8·106 N ; ΔT = 200 K ; l2 = 450 mm ;
Im Finite-Elemente-Baukasten Femset ist das Stabelement mit Temperaturbelastung im Elementkatalog enthalten. Außerdem gibt es eine Interface-Routine elemat_m, mit der die Berechnung aus dem Command Window von Matlab gestartet werden kann. Dieser Routine müssen drei Parameter übergeben werden:
- Anzahl der Freiheitsgrade der Elementknoten (hier: 2),
- Matrix mit den Koordinaten der Knoten, hier: Koordinaten der Knoten 2 und 4,
- Vektor mit den Element-Parametern, hier sind es zwei Werte: Dehnsteifigkeit EA2 und Temperaturbelastung αt ΔT.
Aus diesen Angaben kann Femset den Typ des Elements bestimmen. Mit der nachfolgend zu sehenden Kommandozeile wird die Elementsteifigkeitsbeziehung berechnet und in das Command Window ausgegeben.
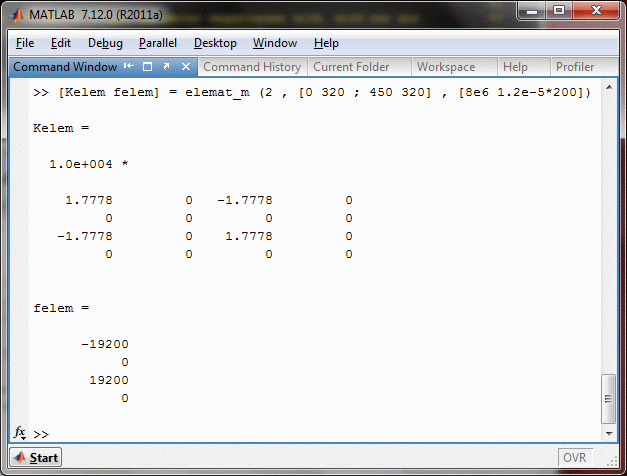
Das Ergebnis für den Vektor der reduzierten Elementlasten entspricht der Vorstellung: Stab 2 will sich ausdehnen und bringt dabei horizontal gerichtete Kräfte auf das Lager am Knoten 2 (nach links gerichtet) und auf den Knoten 4 (nach rechts gerichtet) auf.
Unter TM-interaktiv existiert ein Programm "Statisch unbestimmte ebene Fachwerke (FEM)", das auf der Basis des hier vorgestellten Elements arbeitet.

