FEMSET ist ein Finite-Elemente-"Baukasten", der die Gerüste verschiedener FEM-Solver enthält, die beliebig erweitert werden können, auch und besonders um neue Element-Typen. Es sind jedoch einige Elemente vordefiniert, so dass auch ohne Programmierung einer Element-Beziehung ein komplettes FEM-Programm erzeugt werden kann. Das wichtigste Merkmal aller vordefinierten und auch zusätzlich erzeugten Elementtypen ist die ...
Element-Charakteristik
Ein finites Element wird in FEMSET durch vier charakteristische Zahlenwerte ("Element-Charakteristik") definiert und/oder durch eine Typnummer identifiziert. Wenn keine Typnummer angegeben ist, versucht FEMSET, den Typ aus der "Element-Charakteristik kx, kf, ke, kp" zu entnehmen:
- kx - Koordinaten pro Knoten (zulässige Werte: 1, 2 oder 3): Dieser Parameter legt fest, ob ein ein-, zwei- oder dreidimensionales Problem mit dem Elementtyp behandelt werden kann.
- kf - Freiheitsgrade pro Knoten: Dieser Parameter bestimmt gemeinsam mit dem folgenden Parameter ke die "Qualität" des finiten Elements. Die Anzahl der Freiheitsgrade eines Knotens ist bei elastostatischen Problemen gleich der primär für diesen Knoten anfallenden Ergebnisse (Verformungen) und der für den Knoten vorgebbaren Knotenlasten.
- ke - Anzahl der Knoten pro Element.
- kp - Anzahl der vorzugebenden Elementparameter: Dies können geometrische Parameter (Querschnitt, Dicke, ...), Materialeigenschaften (Elastizitätsmodul, Querkontraktionszahl, t hermischer Ausdehnungskoeffizient, Massebelegung, ...) oder Elementlasten (Linienlasten, Flächenlasten, Volumenlasten, Temperaturerhöhung, ...) sein. Es sind genau die Parameter, die für den Aufbau der Elementbeziehung erforderlich sind.
Es ist in der Regel (und für die vordefinierten Elementtypen immer) möglich, aus diesen 4 Werten den Elementtyp zu bestimmen. Weil in Femset die Koordinaten der Elementknoten immer aus der Matrix der Knotenkoordinaten entnommen werden, sind für den Aufbau der Elementbeziehungen nur noch die kp Elementparameter erforderlich.
Vordefinierte Elementtypen für elastostatische Berechnungen
Vordefinierte Elementtypen für die Berechnung von Eigenschwingungen
|
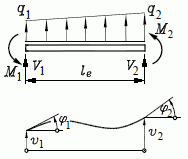
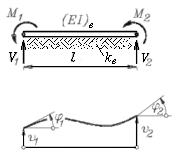
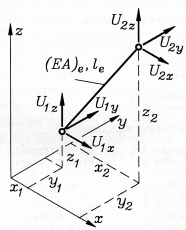
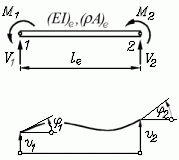
Ebenes biegesteifes Element (Bd2DKM, Schlüssel: 10015) |
kx = 1 kf = 2 ke = 2 kp = 2 |
Weil mit den Knotenkoordinaten auch die Elementlänge le bekannt ist, werden nur zwei Elementparameter benötigt: Biegesteifigkeit EI, Dehnsteifigkeit EA und Massebelegung ρA (Masse pro Länge). Theoretische Grundlagen: "J. Dankert: Numerische Methoden der Mechanik", Kapitel "Die Methode der finiten Elemente". |
|
|
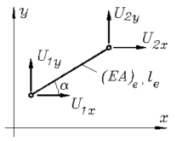
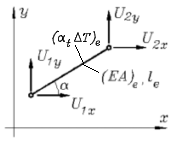
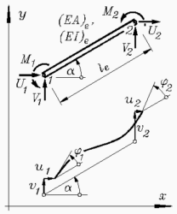
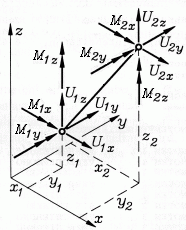
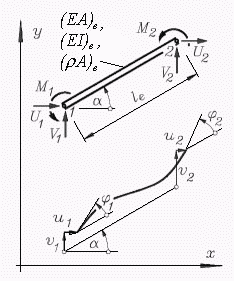
Ebenes biege- und dehnsteifes Rahmen-Element (Bm2DKM, Schlüssel: 10020) |
kx = 2 kf = 3 ke = 2 kp = 3 |
Weil mit den Knotenkoordinaten auch die Elementlänge le und der Winkel α bekannt sind, werden nur drei Elementparameter benötigt: Biegesteifigkeit EI und Massebelegung ρA (Masse pro Länge). Theoretische Grundlagen: "J. Dankert: Numerische Methoden der Mechanik", Kapitel "Die Methode der finiten Elemente". |
|
Vordefinierte Elementtypen für spezielle Probleme
|
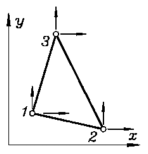
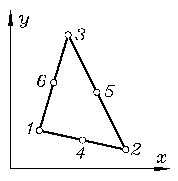
Ebenes Sechs-Knoten-Element für die Torsionsberechnung TORSD6 (Tors3_6, Schlüssel: 2036) |
kx = 2 kf = 1 ke = 6 kp = 0 |
Weil mit den Knotenkoordinaten auch die Geometrie des Elements bekannt ist, werden keine weiteren Elementparameter benötigt. Theoretische Grundlagen: "Dankert/Dankert: Technisch Mechanik", Kapitel "Methode der finiten Elemente". |
|