Am Beispiel eines einfachen Biegeträgers sollen der Aufbau der Elementmatrizen, der Zusammenbau zu den Systemmatrizen, der Einbau der geometrischen Randbedingungen und die Lösung des Eigenwertproblems (Berechnung der Eigenfrequenzen und der Eigenschschwingungsformen) demonstriert werden.
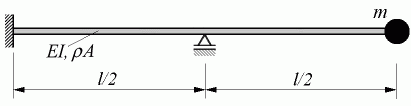 Aufgabe: Für den nebenstehend skizzierten Träger mit konstanter Biegesteifigkeit und konstanter Massebelegung (und einer zusätzlichen Einzelmasse am freien Ende) sollen die beiden kleinsten Eigenfrequenzen der Biegeschwingung und die zugehörigen Eigenschwingungsformen berechnet werden.
Aufgabe: Für den nebenstehend skizzierten Träger mit konstanter Biegesteifigkeit und konstanter Massebelegung (und einer zusätzlichen Einzelmasse am freien Ende) sollen die beiden kleinsten Eigenfrequenzen der Biegeschwingung und die zugehörigen Eigenschwingungsformen berechnet werden.
Gegeben: EI = 3000 Nm2 ; ρA = 3 kg/m ; m = 2 kg ; l = 1 m .
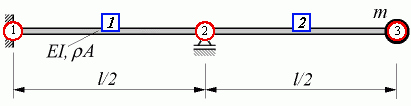 Der Träger wird in nur 2 finite Elemente unterteilt, dabei entstehen 3 Knoten. Die nebenstehende Skizze zeigt die gewählte Nummerierung.
Der Träger wird in nur 2 finite Elemente unterteilt, dabei entstehen 3 Knoten. Die nebenstehende Skizze zeigt die gewählte Nummerierung.
Auch für die Eigenschwingungsberechnungen gestattet das Matlab-Interface zum Finite-Elemente-Baukasten Femset Einblicke in die Zwischenstufen des Algorithmus. Deshalb wird mit dem nachstehend zu sehenden Matlab-Script zunächst in den Zeilen 5 bis 9 das Berechnungsmodell definiert, danach werden die jeweils zwei Elementmatrizen der beiden Elemente (Zeilen 12 und 13), die Systemmatrizen ohne (Zeilen 15 bis 17) bzw. mit Berücksichtigung der Randbedingungen (Zeilen 19 bis 21) berechnet und in das Command Window ausgegeben. Abschließend wird das Matrizeneigenwertproblem gelöst (Zeile 24).
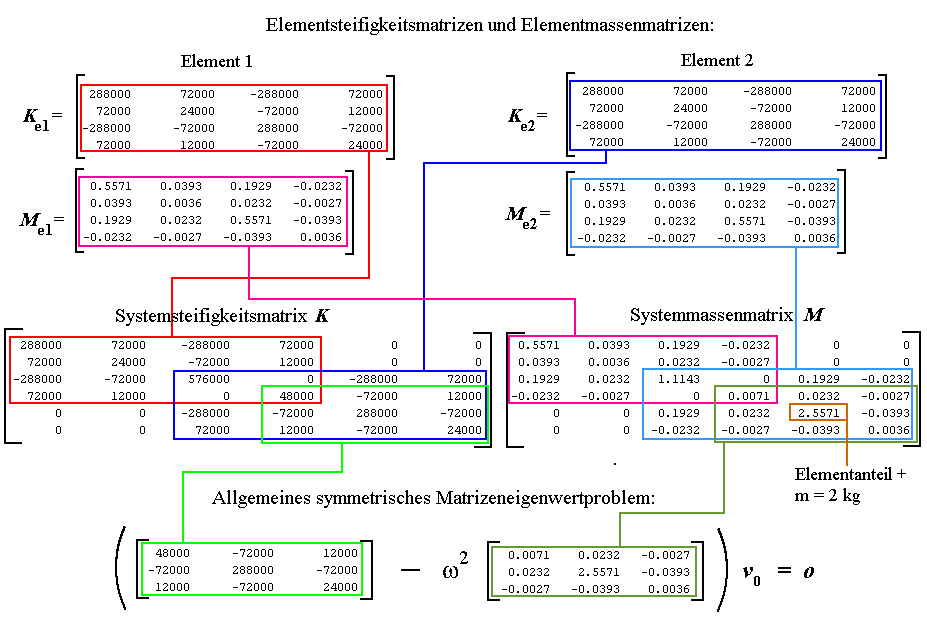
 Das Berechnungsmodell: In xy stehen die Koordinaten der 3 Knoten, bezogen auf ein (beliebiges) hier im Knoten 1 liegendes Koordinatensystem, km ("Koinzidenzmatrix") enthält die Zuordnung der Knoten zu den Elementen (zu Element 1 gehören Knoten 1 und 2, zu Element 2 die Knoten 2 und 3). In der Elementparametermatrix ep stehen in jeder Zeile 2 Werte für ein Element: Biegesteifigkeit EI und Massebelegung ρA. Die Matrix der Randbedingungen kr signalisiert für die jeweils zwei Freiheitsgrade der Knoten (Vertikalverschiebung, Biegewinkel) mit einer 1 eine "verhinderte Verschiebung", mit einer 0 die freie Verschiebungsmöglichkeit. In der Matrix der diskreten Massen mn können analog dazu für jeden Knoten eine Einzelmasse und ein Massenträgheitsmoment definiert werden.
Das Berechnungsmodell: In xy stehen die Koordinaten der 3 Knoten, bezogen auf ein (beliebiges) hier im Knoten 1 liegendes Koordinatensystem, km ("Koinzidenzmatrix") enthält die Zuordnung der Knoten zu den Elementen (zu Element 1 gehören Knoten 1 und 2, zu Element 2 die Knoten 2 und 3). In der Elementparametermatrix ep stehen in jeder Zeile 2 Werte für ein Element: Biegesteifigkeit EI und Massebelegung ρA. Die Matrix der Randbedingungen kr signalisiert für die jeweils zwei Freiheitsgrade der Knoten (Vertikalverschiebung, Biegewinkel) mit einer 1 eine "verhinderte Verschiebung", mit einer 0 die freie Verschiebungsmöglichkeit. In der Matrix der diskreten Massen mn können analog dazu für jeden Knoten eine Einzelmasse und ein Massenträgheitsmoment definiert werden.
Weil die Ergebnisse (Eigenkreisfrequenzen) in der Dimension die Zeit enthalten, die bei den Größen des Berechnungsmodells gar nicht vorkommt, gilt die dringende (und hier natürlich eingehaltene) Empfehlung: Für das Berechnungsmodell sollten konsequent die Einheiten kg, N und m für alle Werte verwendet werden. Dann erhält man die Eigenkreisfrequenzen mit der Dimension s−1.
Alle Ergebnisse werden in das Command Window ausgegeben. Sie wurden im folgenden Bild mit Erläuterungen so zusammengestellt, dass man die Zusammenhaänge zwischen den einzelnen Matrizen erkennen kann.
Weil beide Elemente (mit gleichen Abmessungen und Materialeigenschaften) identisch sind, sind auch ihre Elementsteifigkeitsmatrizen bzw. Elementmassenmatrizen gleich. Man sieht, dass die Elementmatrizen direkt auf die entsprechenden Positionen in die Systemmatrizen eingespeichert werden. Au f den Positionen, auf die Anteile aus verschiedenen Elementmatrizen gelangen (hier sind es die Bereiche, die zum Knoten 2 gehören), werden diese addiert. Anschließend wurde in der Systemmassenmatrix auf dem ersten der beiden zum Knoten 3 gehörenden Hauptdiagonalelemente die Zusatzmasse m = 2 kg ergänzt.
In den Systemmatrizen ( K und M) sind zunächst die geometrischen Randbedingungen (verhinderte Verschiebungen) unberücksichtigt. Am Knoten 1 sind beide Verschiebungen (Vertikalverschiebung, Biegewinkel), am Knoten 2 nur die Vertikalverschiebung verhindert. Weil für Eigenwertprobleme das Berücksichtigen der verhinderten Verschiebungen durch "Zeilen-Spalten-Streichen" zu empfehlen ist, ist diese Strategie auch in Femset realisiert. Das bedeutet, dass in beiden Systemmatrizen K und M die ersten 3 Zeilen und die ersten 3 Spalten zu streichen sind. Es verbleibt das allgemeine symmetrische Matrizeneigenwertproblem mit zwei (3*3)-Matrizen.
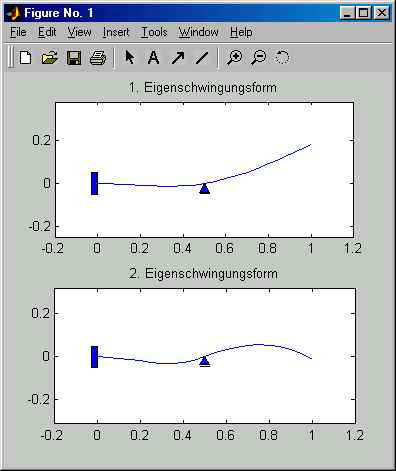 Nach der Lösung des Matrizeneigenwertproblem (Zeile 24 im Matlab-Script) werden die Eigenkreisfrequenzen in Zeile 25 auf Frequenzen umgerechnet und in das Command Window ausgegeben. In Zeile 26 werden die beiden Eigenschwingungsformen in ein Graphik-Fenster gezeichnet (nebenstehendes Bild).
Nach der Lösung des Matrizeneigenwertproblem (Zeile 24 im Matlab-Script) werden die Eigenkreisfrequenzen in Zeile 25 auf Frequenzen umgerechnet und in das Command Window ausgegeben. In Zeile 26 werden die beiden Eigenschwingungsformen in ein Graphik-Fenster gezeichnet (nebenstehendes Bild).
Die Ergebnisse im Command Window
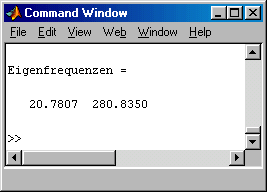
können mit den exakten Werten verglichen werden, weil dieses einfache Beispiel einer Lösung der Schwingungsdifferenzialgleichung für den geraden massebehafteten Träger zugänglich ist:
f1,exakt = 20,78 s−1 ; f2,exakt = 242,13 s−1 .
Die Schlussfolgerungen sind verallgemeinerungsfähig: Während die erste Eigenfrequenz schon mit zwei Elementen hervorragend angenähert wird, zeigt schon die zweite Eigenfrequenz erhebliche Abweichungen vom exakten Wert. Die Finite-Elemente-Methode ist ein Näherungsverfahren, und die Ergebnisse sind immer nur so gut, wie die Ansatzfunktionen in der Lage sind, die exakten Verformungen anzunähern. Bei einer Rechnung mit mehr als zwei Elementen werden auch die Ergebnisse für die höheren Frequenzen sehr schnell besser. Schon bei einer Einteilung der Trägerlänge in 8 Elemente erhält man auch für den 2. Eigenwert mit
f2 = 242,21 s−1
einen ausgezeichneten Näherungswert.
Unter TM-interaktiv existiert ein Programm "Eigenschwingungen ebener Rahmen", das die hier betrachteten Biegeträger als Sonderfall enthält (es arbeitet auf der Basis der hier verwendeten Ansatzfunktion). Damit kann das behandelte Beispiel nachgerechnet werden.

