Wegweiser
Die beiden Möglichkeiten, die theoretischen Grundlagen der Finite-Elemente-Methode zu formulieren, werden hier mit unterschiedlichen Zielen demonstriert:
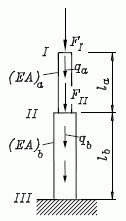
- Am einfachsten denkbaren Beispiel, dem nebenstehend skizzierten elastischen Druckstab, wird mit dem strukturdynamischen Zugang der gesamte Finite-Elemente-Algorithmus erläutert. Die Voraussetzungen, die man benötigt, um diesen Weg zu verstehen sind minimal: Es genügen die Grundkenntnisse der Festigkeitslehre, an und für sich ist es ausreichend, Gleichgewicht von Kräften, die alle auf einer Wirkungslinie liegen, und das Hookesche Gesetz zu kennen. Dieser Weg führt über die "Element-Steifigkeitsbeziehung", das Erzeugen der "System-Steifigkeitsbeziehung", den "Einbau der Randbedingungen" bis zur "Berechnung der Ergebnisse".
- Mit dem mathematischen Zugang zur Finite-Elemente-Methode werden die beiden besonders wichtigen Probleme der Technischen Mechanik behandelt, elasto-statische Systeme und Eigenschwingungen elastischer System. Ausgangspunkte sind jeweils Minimalprinzipien: Prinzip vom Minimum des elastischen Potenzials, das mit Hilfe des Verfahrens von Ritz zum Ziel führt (elastostatisches Problem) und das Hamiltonsche Prinzip, aus dem die FEM-Beziehungen mit Hilfe der Lagrangeschen Bewegungsgleichungen 2. Art hergeleitet werden. Dieser Weg ist etwas anspruchsvoller als der oben beschriebene "strukturdynamische Zugang am einfachsten Beispiel".
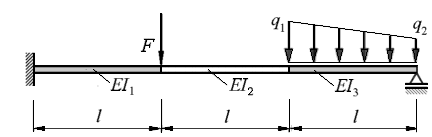
Für den zweiten Weg werden die allgemeinen (dreidimensionalen) Grundgleichungen formuliert und jeweils parallel an einem einfachen eindimensionalen System demonstriert. Hier geht es ...
- ... zur allgemeinen Formulierung der Beziehungen für das elasto-statische Problem, ...
- ... das hier an dem nebenstehend skizzierten Biegeträger demonstriert wird.
Hier geht es ...
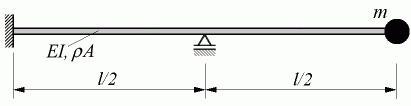
- ... zur allgemeinen Formulierung der Beziehungen für dynamische Probleme bei elasto-statischen Problemen, ...
- ... das hier am Beispiel der Berechnung der Eigenschwingungen des nebenstehend skizzierten Biegeträgers demonstriert wird.

