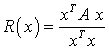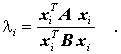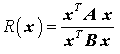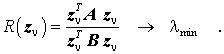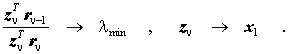Vektoriteration für das Allgemeine Eigenwertproblem

Das Allgemeine Matrizeneigenwertproblem

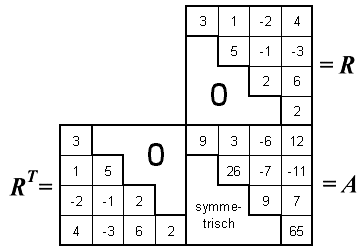
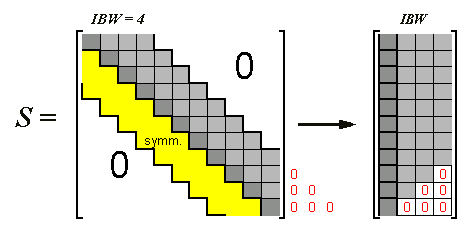
kann, wenn B regulär ist, auf ein Spezielles Matrizeneigenwertproblem zurückgeführt werden (siehe " Allgemeines → Spezielles Matrizeneigenwertproblem "). Bei symmetrische Matrizen A und B sollte unbedingt die Symmetrie erhalten bleiben. Ist die symmetrische Matrix B auch noch positiv definit (typisch für die meisten Mechanik-Probleme), so gelingt dies nach dem hier vorgestellten Verfahren. Während die Symmetrie des Matrizeneigenwertproblems erhalten bleibt, geht eine eventuell vorhandene Bandstruktur der Matrix A dabei jedoch verloren, was für die Eigenwertprobleme mit großen Matrizen, wie sie für die Finite-Elemente-Methode typisch sind, ein erheblicher Nachteil sein kann.

Deshalb werden für das Allgemeine Matrizeneigenwertproblem mit symmetrischen Bandmatrizen Verfahren bevorzugt, die ohne vorherige Transformation auf ein Spezielles Matrizeneigenwertproblem auskommen. Die Verfahren der Vektoriteration (siehe "Vektoriteration nach von Mises" und "Eigenwerte der Inversen, inverse Vektoriteration"), mit denen die für die Technische Mechanik besonders wichtige Aufgabe, die kleinsten Eigenwerte zu berechnen, besonders effektiv erledigt wird, kann so modifiziert werden, dass sie direkt auf das Allgemeine Matrizeneigenwertproblem angewendet werden können.

Auf der Seite "Allgemeines → Spezielles Matrizeneigenwertproblem" wird gezeigt, dass (bei regulärer Matrix B) das Allgemeine Matrizeneigenwertproblem durch Linksmultiplikation mit B⁻¹ auf ein Spezielles Matrizeneigenwertproblem (bei Verlust der Symmetrie) zurückgeführt werden kann:

Auf der Seite "Eigenwerte der Inversen, inverse Vektoriteration" wird gezeigt, dass die Iteration

(bei beliebigem Startvektor z₀) gegen den Eigenvektor des kleinsten Eigenwertes der Matrix B⁻¹A konvergiert. Durch Linksmultiplikation mit B wird daraus direkt die Iterationsvorschrift für das Allgemeine Matrizeneigenwertproblem:

Ausgehend von einem beliebigen Startvektor z₀, wird in jedem Iterationsschritt eine Multiplikation des Vektors mit B mit anschließender Lösung eines linearen Gleichungssystems ausgeführt:

Dieses Verfahren konvergiert gegen den Eigenvektor des kleinsten Eigenwerts: z_ν---> x₁.

Da sich die Koeffizientenmatrix des Gleichungssystems während der Iteration nicht ändert, muss die Dreieckszerlegung (z. B. nach Cholesky ) nur einmal ausgeführt werden. Symmetrie und Bandstruktur der Matrizen bleiben bei diesem Iterationsprozess erhalten.

Der Rayleighsche Quotient , mit dem auch hier der Eigenwert berechnet werden sollte, ergibt sich für das Allgemeine Matrizeneigenwertproblem mit symmetrischen Matrizen aus entsprechenden Überlegungen wie für das Spezielle Matrizeneigenwertproblem. Ein Eigenvektor x_i muss offensichtlich der Beziehung

genügen. Multipliziert man diese Gleichung auf beiden Seiten von links mit dem transponierten Eigenvektor entsprechend

so steht auf der rechten Seite eine quadratische Form, durch die dividiert werden kann, und man erhält:

Ein Ausdruck mit symmetrischen Matrizen A und B der Form

wird als Rayleighscher Quotient des Allgemeinen symmetrischen Matrizeneigenwertproblems bezeichnet. Für einen Eigenvektor nimmt er den Wert des zugehörigen Eigenwertes an, und es lässt sich zeigen, dass er den Eigenwert für Vektoren x, die eine recht grobe Näherung eines Eigenvektors sind, schon sehr gut annähert.

Deshalb ist es empfehlenswert, die Näherungsberechnung des Eigenwertes mit dem Rayleigh-Quotienten auszuführen, zumal der aufwändige Teil (Multiplikationen Matrix · Vektor) ohnehin in jedem Iterationsschritt ausgeführt werden muss:

Mit den Vereinfachungen, die sich durch die doppelt verwendbaren Zwischenergebnisse ergeben, gilt also folgende