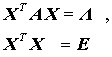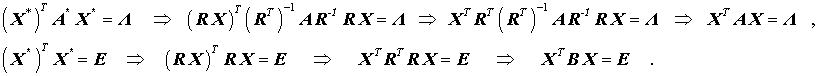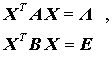Symmetrische Matrizeneigenwertprobleme

Das Spezielle Matrizeneigenwertproblem mit symmetrischer Matrix

Für den besonders wichtigen Spezialfall des Speziellen Matrizeneigenwertproblems

mit symmetrischer (reeller) Matrix A gilt:

• Alle Eigenwerte sind reell (und positiv, wenn A auch noch positiv definit ist).
   
• Es existiert eine Ähnlichkeitstransformation

mit der Orthonormalmatrix X (so genannte Modalmatrix), deren Spalten die normierten Eigenvektoren der Matrix A enthalten, und der Diagonalmatrix Λ (so genannte Spektralmatrix), deren Diagonalelemente die Eigenwerte von A sind (E ist die Einheitsmatrix).

Es lohnt sich im Allgemeinen, auch erheblichen Mehraufwand bei der Formulierung des Matrizeneigenwertproblems in Kauf zu nehmen, um zu symmetrischen Matrizen zu kommen, weil neben geringerem Aufwand für die Lösung auch eine Reihe von numerischen Schwierigkeiten damit vermieden werden können. Wenn beim Allgemeinen Matrizeneigenwertproblem

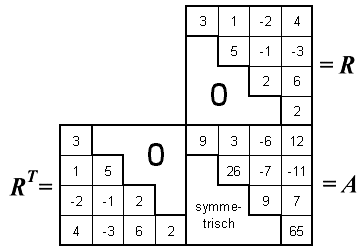
beide Matrizen A und B symmetrisch sind, sollte man entweder bei der Überführung in ein Spezielles Matrizeneigenwertproblem möglichst die Symmetrie zu erhalten versuchen oder bei der Auswahl des Lösungsverfahrens darauf achten, dass die Vorteile der symmetrischen Matrizen ausgenutzt werden können. Wenn mit Hilfe der Cholesky-Zerlegung von B die Überführung in ein Spezielles Matrizeneigenwertproblem unter Wahrung der Symmetrie gelingt, dann gilt

Für die mit Stern gekennzeichneten Größen gelten natürlich auch die Formeln der oben angegebenen Ähnlichkeitstransformation, und man berechnet (X^* ist wie oben die Zusammenfassung aller Eigenvektoren spaltenweise zu einer quadratischen Matrix):

Damit hat man die folgenden Aussagen gewonnen:

Das Allgemeine Matrizeneigenwertproblem mit symmetrischen Matrizen

Für das Allgemeine Matrizeneigenwertproblem

mit symmetrischen (reellen) Matrizen A und B gilt:

• Alle Eigenwerte sind reell (und positiv, wenn A und B auch noch positiv definit sind).
   
• Es existiert eine Ähnlichkeitstransformation

mit der Matrix X, deren Spalten die Eigenvektoren des Allgemeinen Matrizeneigenwertproblems enthalten, und der Diagonalmatrix Λ, deren Diagonalelemente die Eigenwerte sind. Man beachte, dass sich diese Aussage von der über das Spezielle Matrizeneigenwertrproblem nur dadurch unterscheidet, dass die Eigenvektoren "B-orthonormal" sind.