|
Der QR-Algorithmus Zu jeder (reellen) Matrix A existiert eine so genannte QR-Zerlegung
mit einer Orthogonalmatrix Q und einer
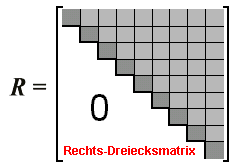
Rechtsdreiecksmatrix
Auf der Basis der QR-Zerlegung für quadratische Matrizen existiert ein sehr einfacher Algorithmus für das Erzeugen der
Schurschen Form
Jeder Iterationsschritt besteht also aus einer QR-Zerlegung und einer anschließenden Matrixmultiplikation. Die Matrizen Hk konvergieren gegen die Schursche Form der Matrix A, deren Hauptdiagonalelemente die Eigenwerte der Matrix A sind (bei konjugiert komplexen Eigenwertpaaren repräsentiert ein 2*2-Hauptdiagonalblock diese beiden Eigenwerte). |
|
Reduzierung einer Matrix auf Hessenberg-Form
Dies wird erreicht durch
Ähnlichkeitstransformationen mit elementaren Orthogonalmatrizen
genügt. Im Gegensatz zum Jacobi-Verfahren, bei dem mit einer p-q-Transformation das Element aq,p zu Null wird, ist es bei der Givens-Rotation das linke Nachbarelement. Dies hat den Vorteil, dass (im Gegensatz zum Jacobi-Verfahren) durch geeignete Wahl der Reihenfolge der Transformationen bereits erzeugte Nullen nicht wieder zerstört werden, hat allerdings den Nachteil, dass die Nebendiagonale unterhalb der Hauptdiagonalen auf diesem Wege nicht zu Null gemacht werden kann.
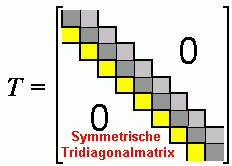
Bei symmetrischen Matrizen entstehen die Null-Elemente automatisch auch im rechten oberen Bereich der Matrix, so dass das Ergebnis schließlich eine so genannte symmetrische Tridiagonalmatrix ist. Der oben angegebene QR-Algorithmus wird also in dem Sinne modifiziert, dass die erste Zeile, die die Startmatrix für die Iteration festlegt, durch die Hessenberg-Transformation der Matrix A ersetzt wird. |
|
Demonstration der Aussagen an einem Beispiel
Im nebenstehend zu sehenden Script werden die beiden symmetrischen Matrizen des Allgemeinen Matrizeneigenwertproblems in den Zeilen 3 bis 17 aufgebaut. In Zeile 22 wird daraus die unsymmetrische Matrix Aq, in Zeile 28 wird die symmetrische Matrixd As eines jeweils äquivalenten Speziellen Matrizeneigenwertproblems erzeugt (siehe dazu: "Allgemeines → Spezielles Matrizeneigenwertproblem"). In Zeile 30 werden beide Matrizen in die Hessenberg-Form transformiert (und in das Command Window ausgegeben). In den Zeilen 31 bis 34 werden für beide Matrizen 20 Iterationsschritte des oben beschriebenen QR-Algorithmus ausgeführt, die die Matrizen in die
Schursche Form
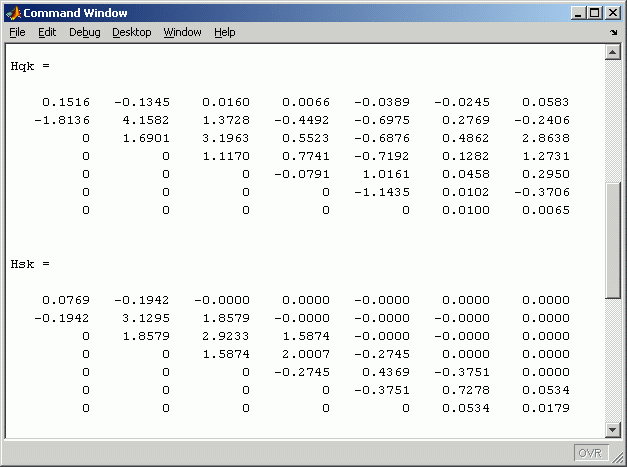
Nachstehend ist zunächst ein Ausschnitt des Command Windows zu sehen, der die in der Zeile 30 ermittelten Hessenberg-Formen zeigt. Die aus der unssymmetrischen Matrix Aq erzeugte Matrix Hqk zeigt die typische Besetzung mit von Null verschiedenen Elementen ("Rechtsdreiecksmatrix + Nebendiagonale"). Die aus der symmetrischen Matrix As erzeugte Hessenberg-Matrix Hsk ist eine symmetrische Tridiagonalmatrix:
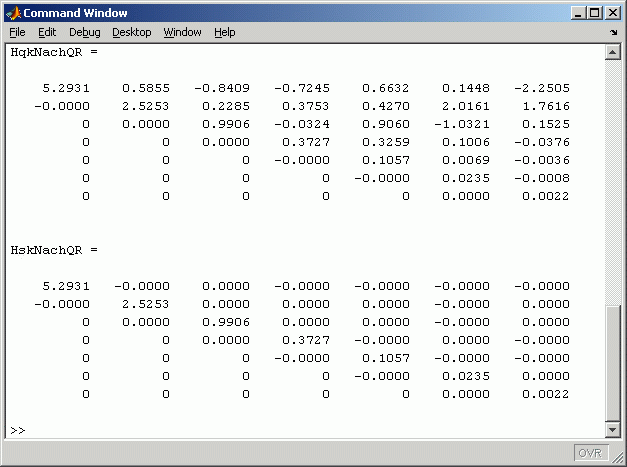
Nach 20 Iterationsschritten des QR-Algorithmus zeigen die Matrizen
Schursche Form
|

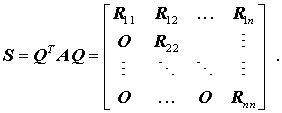
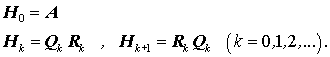
 Der Aufwand für die oben beschriebene
Der Aufwand für die oben beschriebene 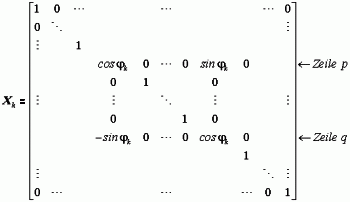
 Wenn man z. B. die Nullen unterhalb der Nebendiagonalen spaltenweise von links nach rechts erzeugt, kommt man nach genau (
Wenn man z. B. die Nullen unterhalb der Nebendiagonalen spaltenweise von links nach rechts erzeugt, kommt man nach genau (