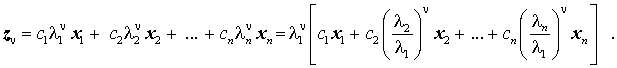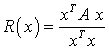Vektoriteration nach von Mises

Bei der Behandlung des speziellen Matrizeneigenwertproblems

interessieren meist nur einige wenige Eigenwerte und die zugehörigen Eigenvektoren (z. B. die Knick- oder Beullast oder die kleinsten Frequenzen eines Schwingungssystems). Die nachfolgend beschriebene von-MISESsche Vektoriteration liefert unmittelbar den betragsgrößten (dominanten) Eigenwert nebst Eigenvektor. Unter den zahlreichen Modifikationen des Vefahrens sind besonders diejenigen interessant, die nacheinander oder gleichzeitig mehrere Eigenwerte berechnen und die Verfahren, die die betragskleinsten Eigenwerte finden.

Die folgenden Überlegungen gehen davon aus, dass die Matrizen n verschiedene Eigenvektoren besitzen und auch dann nur reelle Eigenwerte haben, wenn die Symmetrie der Matrix A nicht vorausgesetzt wird.

Beginnend mit einem beliebigen Startvektor z₀ wird die Folge der so genannten iterierten Vektoren

gebildet. Denkt man sich z₀ nach den (natürlich nicht bekannten) Eigenvektoren x_i entwickelt, so ergibt sich aus

für den iterierten Vektor:

Nach der Definition des speziellen Matrizeneigenwertproblems gilt für jeden Eigenvektor x_i

bzw.

Damit kann der iterierte Vektor folgendermaßen aufgeschrieben werden:

Ist nun λ₁ der betragsgrößte aller Eigenwerte, so konvergiert der iterierte Vektor gegen

bzw.

Jede Komponente des Vektors z_ν+1 ist das λ₁-fache der Komponente von z_ν , und die Folge der iterierten Vektoren selbst konvergiert gegen den zugehörigen Eigenvektor. Die Konvergenz ist offensichtlich wesentlich davon abhängig, dass der absolut zweitgrößte Eigenwert deutlich kleiner ist als der absolut größte.

Theoretisch ist die Konvergenz zum dominanten Eigenwert nur gesichert, wenn der Startvektor z₀ nicht zufällig orthogonal zu  x₁ ist, weil dann der Koeffizient c₁ = 0 wäre. Praktisch ist dies kaum eine Gefahr, weil nach einigen Schritten durch die unvermeidlichen Rundungsfehler sicher auch eine (zunächst sehr kleine) Komponente von x₁ in die iterierten Vektoren hineinkommt, was dann doch zur Konvergenz gegen den betragsgrößten Eigenwert und den zugehörigen Eigenvektor führt.

Die Zahlenwerte der Komponenten der iterierten Vektoren können sehr schnell unangenehm groß oder klein werden (je nachdem, ob der Betrag von λ₁ größer oder kleiner als 1 ist). Da es nur auf das Verhältnis der Komponenten zweier aufeinander folgender iterierter Vektoren ankommt, empfiehlt sich nach jedem Schritt eine geeignete Normierung des iterierten Vektors.

Siehe auch: Modifikation dieses Verfahrens mit dem Rayleigh-Quotienten und Beispiel für die von-Mises-Iteration unter Ausnutzung des Rayleigh-Quotienten.