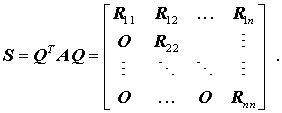Die Aufgabenstellungen

Weil praktisch nur iterative Verfahren zur Lösung des Speziellen Matrizeneigenwertproblems

SEWP07

verfügbar sind, sollte man die beiden folgenden Aufgabenstellungen unterscheiden und danach die Verfahrensauswahl treffen:

  • Die Lösung des vollständigen Matrizeneigenwertproblems liefert sämtliche Eigenwerte (und bei Bedarf auch die zugehörigen Eigenvektoren).
     
  • Häufig (und bei typischen Ingenieurproblemen sogar sehr häufig) genügt die Kenntnis eines Eigenwertes oder einiger weniger Eigenwerte (und der zugehörigen Eigenvektoren) am Rand des Spektrums (in der Regel die kleinsten Eigenwerte), diese Aufgabe wird auch als partielles Matrizeneigenwertproblem bezeichnet.

Der Satz von Schur (für reelle Matrizen)

Für jede reelle Matrix A existiert eine Orthogonalmatrix Q, mit der eine Ähnlichkeitstransformation eine quasi-obere Dreiecksmatrix ergibt (Schursche Matrix):

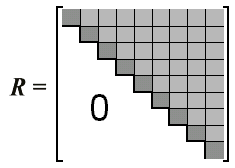
Eine spezielle Ähnlichkeitstransformation einer reellen Matrix führt auf Schursche Matrix

Dabei stehen auf der Hauptdiagonalen die Eigenwerte der Matrix A. Für die reellen Eigenwerte sind die Rii einfache Matrixelemente. Die komplexen Eigenwerte werden jeweils durch einen 2*2-Block Rii repräsentiert. Für den wichtigen Sonderfall, dass die Matrix A nur reelle Eigenwerte besitzt, ist also die Schursche Matrix eine reine Rechtsdreiecksmatrix

Wichtiger Spezialfall: Für eine symmetrische Matrix A degeneriert die Schursche Matrix zur reinen Diagonalmatrix mit den Eigenwerten als Diagonalelementen (symmetrische Matrizen haben nur reelle Eigenwerte).

Die iterative Umformung der Matrix A mit dem Ziel des Erzeugens der Schurschen Matrix ist die typische Strategie für die Lösung des vollständigen Matrizeneigenwertproblems . Ein besonders effektiver Vertreter dieser Verfahren wird auf der Seite
Hessenberg-Form und QR-Algorithmus "vorgestellt.

Vektoriteration

Die Basis für die Verfahren, die das partielle Matrizeneigenwertproblem lösen, ist die auf Richard von Mises zurückgehende Überlegung, dass eine mit einem beliebigen Startvektor z0 gestartete Vektorfolge

Folge der iterierten Vektoren nach von Mises

gegen den Eigenvektor des betragsgrößten Eigenwertes der Matrix A konvergiert und die Verhältnisse beliebiger Komponenten der so genannten iterierten Vektoren gegen den Wert des zugehörigen Eigenwertes konvergieren (warum das so ist, wird auf der Seite "Vektoriteration nach von Mises" gezeigt).

Für dieses Verfahren existieren zahlreiche Modifikationen, besonders wichtig sind:

  • Die inverse Vektoriteration ermittelt den Eigenvektor des betragskleinsten Eigenwertes (und natürlich den Eigenwert selbst), siehe: "Eigenwerte der Inversen, inverse Vektoriteration".
     
  • Man kann das Verfahren so modifizieren, dass es direkt mit dem Allgemeinen Matrizeneigenwertproblem arbeitet (ohne vorherige Reduktion auf das Spezielle Matrizeneigenwertproblem), siehe: "Vektoriteration für das Allgemeine Matrizeneigenwertproblem".
     
  • Die Simultaniteration liefert gleichzeitig mehrere Eigenvektoren und Eigenwerte am Rande des Spektrums. Dass diese Strategie auch als inverse Iteration ausgeführt werden kann (und damit die kleinsten Eigenwerte liefert) und auch direkt mit dem Allgemeinen Matrizeneigenwertproblem arbeiten kann (und welche Vorteile dies bietet), wird auf der Seite "Inverse simultane Vektoriteration (symm. AEWP)" gezeigt.