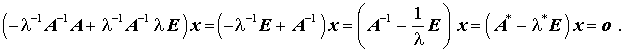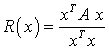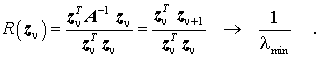Eigenwerte der Inversen, inverse Vektoriteration

Das spezielle Matrizeneigenwertproblem

kann durch Multiplikation (von links) mit -λ⁻¹A⁻¹ wie folgt umgeformt werden:

Das Fazit dieser Umformung lautet: Die zur Matrix A inverse Matrix A⁻¹ hat die gleichen Eigenvektoren wie A bei reziproken Eigenwerten.

Für die von-Mises-Iteration bedeutet dies, dass die Iteration

gegen den Eigenvektor des kleinsten Eigenwertes von A konvergiert. Dies ist eine besonders wichtige Modifikation des Iterationsverfahrens, weil in der Technischen Mechanik in der Regel gerade der kleinste Eigenwert interessiert (Knicklast, Beullast, Grundfrequenz, ...).

Man kann also zur Suche des kleinsten Eigenwertes entweder vorab die Matrix A invertieren oder aber die Iterationsvorschrift entsprechend

modifizieren, so dass in jedem Schritt ein lineares Gleichungssystem gelöst werden muss. Der Aufwand dafür hält sich in Grenzen, weil sich in jedem Schritt nur die rechte Seite des Gleichungssystems ändert, so dass der aufwendige Teil, die Dreieckszerlegung der Matrix A, nur einmal ausgeführt werden muss.

Der Eigenwert wird auch in diesem Fall zweckmäßig mit dem Rayleighschen Quotienten ermittelt, für symmetrische Matrix A z. B. gilt: