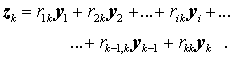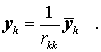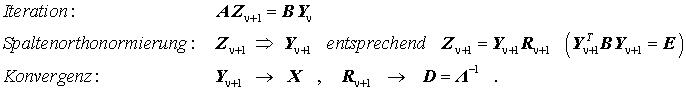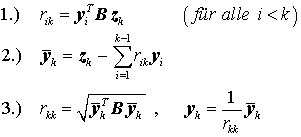|
Problemstellung Während bei Stabilitätsproblemen in der Regel nur der kleinste Eigenwert (Knicklast, Beullast, ...) interessiert, sind bei Schwingungsproblemen neben der Grundfrequenz häufig auch einige weitere der kleinsten Eigenfrequenzen von Interesse. Deshalb wird das Iterationsverfahren zur Berechnung des kleinsten Eigenwerts für das allgemeine Matrizeneigenwertproblem mit symmetrischen Matrizen
hier auf diese Aufgabenstellung erweitert. Zunächst wird daran erinnert, dass für dieses Problem gilt (vgl. die Seite "Symmetrische Matrizeneigenwertprobleme"):
mit der Matrix X, deren Spalten die Eigenvektoren des allgemeinen Matrizeneigenwertproblems enthalten, und der Diagonalmatrix Λ, deren Diagonalelemente die Eigenwerte sind (diese Aussage unterscheidet sich von der über das spezielle Matrizeneigenwertrproblem nur dadurch, dass die Eigenvektoren "B-orthonormal" sind, E ist die Einheitsmatrix). |
|
Inverse Simultaniteration Die Idee der inversen Simultaniteration: Der Iterationsprozess, der für die Berechnung des zum kleinsten Eigenwert gehörenden Eigenvektors führt, wird mit einem Satz von p Vektoren gestartet (p ≤ n, n ist die Zeilen- bzw. Spaltenanzahl der Matrizen A und B). Die Startvektoren werden zu einer Matrix Y0 zusammengefasst. Wenn man nun den inversen Iterationsprozess für einen Vektor so modifiziert, dass er mit dieser Matrix startet (und dann natürlich in jedem Schritt eine Matrix gleichen Formats Yμ erzeugt), würden alle Spalten der Matrix gegen den Vektor des kleinsten Eigenwerts konvergieren. Abhilfe schafft folgende Strategie: Nach jedem Iterationsschritt werden die Spalten der iterierten Matrix "von links nach rechts orthonormiert" (für das allgemeine Matrizeneigenwertproblem natürlich "B-orthonormiert"). Dann konvergiert die (jeweils nur "B-normierte") erste Spalte wieder gegen den Eigenvektor des kleinsten Eigenwerts, die jeweils von allen Komponenten des ersten Eigenvektors "gereinigte" zweite Spalte nach der "von-Mises-Idee" gegen den Eigenvektor des zweitkleinsten Eigenwerts usw. Die Iterationsvorschrift lässt sich also folgendermaßen formulieren:
Das Verfahren konvergiert gegen die Matrix X, deren Spalten die p Eigenvektoren ("B-orthonormiert") zu den p kleinsten Eigenwerten enthalten. Das Problem der Spaltenorthonormierung kann auf unterschiedliche Weise gelöst werden (Orthonormierungsverfahren nach Schmidt, Subspace-Orthonormierung, ...). |
|
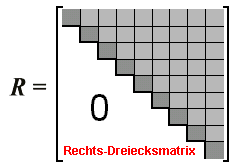
Schmidtsches Orthonormierungsverfahren
mit einer
Rechtsdreiecksmatrix
gilt ("B-orthonormierte" Spalten). Rechts wird dies mit dem
Falkschen Schema
Es wird angenommen, dass die Spalten 1 bis k−1 der Matrix Y bereits orthonormiert sind. Die k−te Spalte von Z muss sich dann aus dem Produkt der ersten k Spalten von Y mit den k Elementen rik der k-ten Spalte von R ergeben:
Wenn man diese Beziehung von links mit yiTB multipliziert, dann fallen auf der rechten Seite wegen der "B-Orthonormiertheit" der Spalten alle Produkte bis auf das mit yi, das den Wert 1 hat, weg:
gestattet die Berechnung aller rik der k-ten Spalte von R für i < k (das Hauptdiagonalelement fehlt noch, weil yk noch nicht bekannt ist). Mit den nunmehr bekannten rik kann die oben angegebene Beziehung folgendermaßen umgestellt werden:
gestattet die Berechnung einer vorläufigen (zu den übrigen Spalten orthogonalen, aber noch nicht normierten) k-ten Spalte der Matrix Y. Die Forderung der "B-Orthonormiertheit" kann so formuliert werden:
Damit kann der noch fehlende Normierungsfaktor nach
berechnet werden und damit die noch fehlende k-te Spalte von Y:
Weil die p Spalten von Y gegen die Eigenvektoren der kleinsten p Eigenwerte konvergieren, werden die rik für i < k (die Elemente oberhalb der Hauptdiagonalen) mit fortschreitender Konvergenz immer kleiner. Diese können ja als "Säuberungsfaktoren" aufgefasst werden, die jeweils alle Komponenten der vorläufigen Eigenvektoren yi mit i < k aus dem vorläufigen Eigenvektor yk herausfiltern. Das bedeutet, dass R gegen eine Diagonalmatrix konvergiert, deren Hauptdiagonalelemente die reziproken Eigenwerte enthalten (vgl. die hier angegebene Iterationsvorschrift). Der hier schrittweise entwickelte Algorithmus wird noch einmal zusammengefasst:
Dieser Algorithmus ist realisiert in einem C-Programm isiasb_m.c, für das ein Interface (Mex-File) existiert, mit dem es aus Matlab aufgerufen werden kann. Eine Beschreibung, ein Beispiel und die Möglichkeit zum Download über diesen Link. |

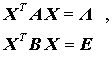
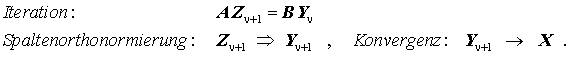
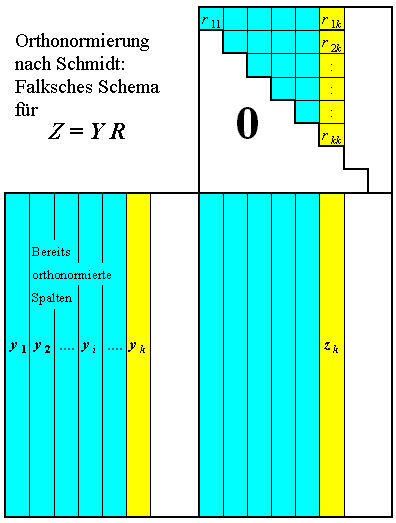 Das Schmidtsche Orthonormierungsverfahren basiert auf der Idee, die Matrix
Das Schmidtsche Orthonormierungsverfahren basiert auf der Idee, die Matrix