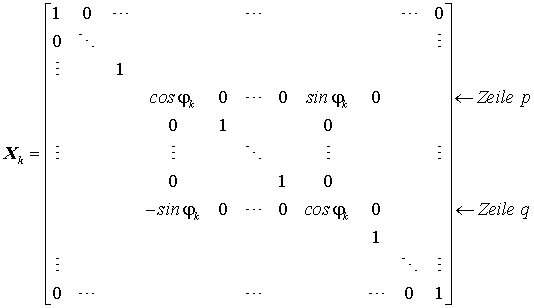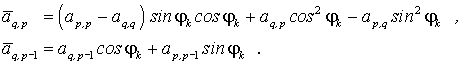|
Elementare Rotationsmatrizen Die Basis verschiedener Verfahren zur Berechnung von Eigenwerten und Eigenvektoren einer Matrix sind elementare Matrizen der Form:
Xk ist eine auf genau vier Positionen modifizierte Einheitsmatrix. Es ist leicht zu verifizieren, dass Xk eine Orthogonalmatrix ist: Sämtliche Spalten (und natürlich auch Zeilen) sind orthogonal zueinander (das jeweilige Skalarprodukt hat den Wert Null), und die Spalten (Zeilen) sind normiert (der Betrag der Vektoren hat den Wert 1). Es gilt also
(E ist die Einheitsmatrix, für Xk gilt also außerdem, dass ihre Inverse gleich der Transponierten ist). Eine Transformation eines Vektors mit einer solchen Matrix entspricht einer Drehung des Bezugssystems (für den zweidimensionalen Fall, bei dem Xk zu einer 2*2-Matrix degeneriert, kann man sich das geometrisch leicht veranschaulichen). Auf der Seite "Inverse Transformation, Ähnlichkeitstransformation" wird gezeigt, dass bei einer solchen Transformation eine beliebige Matrix A durch
zur entsprechenden Matrix im neuen Koordinatensystem wird und dass sich durch diese so genannte Ähnlichkeitstransformation einige Eigenschaften (z. B. die Symmetrie, aber auch die Eigenwerte der Matrix) nicht ändern. Die Verfahren zur Berechnung von Eigenwerten und Eigenvektoren einer Matrix, die mit solchen elementaren Rotationsmatrizen arbeiten, nutzen jeweils die Möglichkeit, durch eine geeignete Wahl des Rotationswinkels φk ein Element der Matrix A bei der Ähnlichkeitstransformation zu Null zu machen, was nachfolgend beschrieben wird. |
|
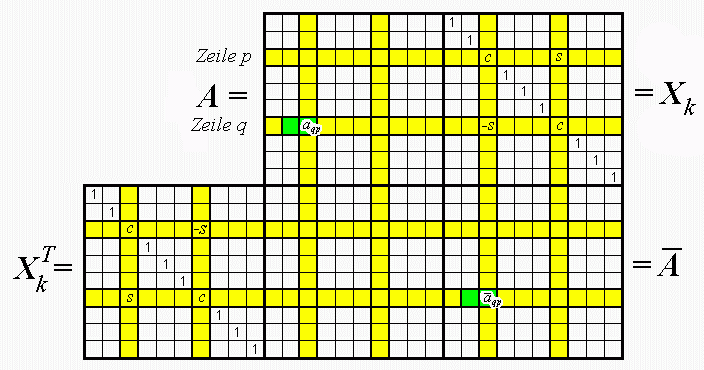
Jacobi-Rotation, Givens-Rotation Eine Ähnlichkeitstransformation mit
einer elementaren Rotationsmatrix, wie sie oben angegeben ist, beeinflusst
nur die Zeilen p und q und die Spalten p und
q der zu transformierenden Matrix. In dem nachfolgend zu
sehenden
Falkschen Schema
Die Formeln, nach denen sich die in den gelb gezeichneten Zeilen und Spalten befindlichen Elemente berechnen, können mit begrenzter Mühe aus dem Schema abgeleitet werden. Von besonderer Bedeutung für verschiedene Verfahren zur Lösung des Matrizeneigenwertproblems ist die Frage nach dem "Schicksal" des Elements aq,p und seines linken Nachbarn. Diese werden zu:
Bei geeigneter Wahl des Winkels φk kann entweder das eine oder das andere Element zu Null gemacht werden:
|