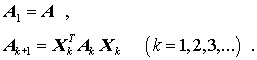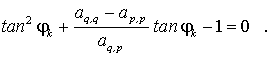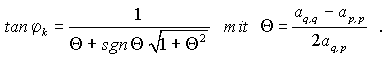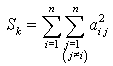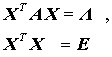Das Verfahren von Jacobi

Das auf den Mathematiker Carl Gustav Jacobi (1804 - 1851) zurückgehende Verfahren zur Berechnung aller Eigenwerte und der zugehörigen Eigenvektoren des speziellen Matrizeneigenwertproblems

mit einer symmetrischen Matrix A arbeitet mit den auf der Seite "Jacobi- und Givens-Rotationen" beschriebenen elementaren Orthogonaltransformationen:

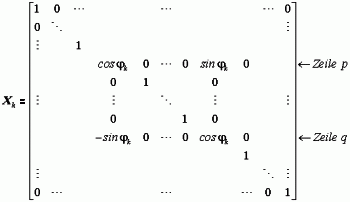
Dabei wird die Transformationsmatrix X_k so gewählt, dass ein Matrixelement a_q,p zu Null wird. Wegen der Symmetrie der Matrix A, die bei Orthogonaltransformationen erhalten bleibt, wird immer auch das Element a_p,q zu Null. Auf der Basis der auf der Seite "Jacobi- und Givens-Rotationen" angegebenen Formel erhält man dafür aus der Bedingungsgleichung

nach einigen elementaren Umformungen eine quadratische Gleichung für tan φ:

 Von den beiden Lösungen dieser Gleichung wird die gewählt, die sich so aufschreiben lässt:

Die sgn-Funktion sorgt dafür, dass im Nenner keine numerische Ziffernauslöschung entsteht. Der Fall a_q,p = 0, für den diese Lösung versagt, braucht nicht weiter betrachtet zu werden, weil in dem Fall die Transformation, die ja genau das Ziel hat, dieses Element zum Verschwinden zu bringen, nicht sinnvoll ist und ausgelassen wird.

Es lässt sich zeigen, dass bei Transformationen dieser Art die Summe der Quadrate der Nichtdiagonalelemente

kleiner wird, so dass sich die Matrizen A_k immer mehr einer Diagonalmatrix annähern. Dass sie tatsächlich und wie schnell sie konvergieren, hängt von der Strategie ab, in welcher Reihenfolge die Nichtdiagonalelemente zum Verschwinden gebracht werden (man beachte, dass bei jedem Schritt vorab bereits erzeugte Nullen wieder verschwinden können).

Beim klassischen Jacobi-Verfahren wird sinnvollerweise jeweils das betragsgrößte Nichtdiagonalement in einem Iterationsschritt zu Null gemacht, das Verfahren konvergiert jedoch auch, wenn in einem Zyklus jeweils alle Nichtdiagonalelemente genau einmal zum Verschwinden gebracht werden (zyklisches Jacobi-Verfahren).

Weil für symmetrische Matrizen eine Ähnlichkeitstransformation

existiert mit der Modalmatrix X, deren Spalten die normierten Eigenvektoren der Matrix A enthalten, und der Diagonalmatrix Λ, deren Diagonalelemente die Eigenwerte von A sind, konvergieren die A_k beim Jacobi-Verfahren gegen eine Diagonalmatrix, deren Hauptdiagonalelemente die Eigenwerte sind. Das Produkt aller elementaren Orthogonalmatrizen X_k konvergiert gegen die Modalmatrix, deren Spalten die zugehörigen Eigenvektoren enthalten.

Der an sich unendliche Prozess des Jacobi-Algorithmus wird abgebrochen, wenn die Nichtdiagonalelemente genügend klein geworden sind. Es lässt sich zeigen, dass zu jedem Diagonalelement a_{i i} einer Matrix A ein Eigenwert λ existiert, so dass

gilt (S_k ist die oben definierte Summe der Quadrate der Nichtdiagonalelemente). Damit ist eine interpretierbare Abbruchschranke verfügbar. Man erkennt an dieser Formel auch einen gewissen Nachteil des Jacobi-Verfahrens: Alle Eigenwerte (und damit auch die meist besonders interessierenden kleinsten Werte) werden mit der gleichen absoluten Genauigkeit geliefert (zumindest für die Größenordnung der Fehler gilt diese Aussage).

Die Eigenwerte bilden sich auf der Hauptdiagonalen in der Regel in ungeordneter Reihenfolge (die Zuordnung der Spalten der Modalmatrix zu den Eigenwerten stimmt aber). Eine dünne Besetzung der Matrix A mit von Null verschiedenen Elementen kann im Allgemeinen nicht mit Vorteil genutzt werden.

Das Jacobi-Verfahren ist ein sehr anschauliches Beispiel für die Transformation einer Matrix mit Orthogonalmatrizen auf eine spezielle Form (hier: Diagonalmatrix) mit dem Ziel, das Matrizeneigenwertproblem zu lösen. Ähnliche Strategien werden für nichtsymmetrische Matrizen verfolgt, die als Sonderfall immer auch den symmetrischen Fall beinhalten. Diese Verfahren findet man auf der Seite "Hessenberg-Form und QR-Algorithmus".