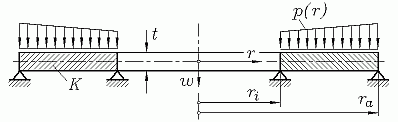
Differenzengleichungen
Auf der Seite "Rotationssymmetrische Kreis- und Kreisringplatten" findet man die Differenzialgleichung, die die Verformung solcher Platten beschreibt:
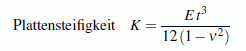
In der Regel sind zwei Randbedingungen am Innen- und zwei Randbedingungen am Außenrand zu formulieren. Dies können (wie bei der Verformungsberechnung des Biegeträgers) Aussagen über die Absenkung w und deren 1. Ableitung nach r und Aussagen über das Biegemoment mr und die Querkraft qr sein. Für diese beiden Schnittgrößen gelten die Formeln:
Mit den auf der Seite "Differenzenverfahren" zusammengestellten zentralen Differenzenformeln können die Differenzialgleichung und die für die Formulierung der Randbedingungen erforderlichen Differenzialbeziehungen als Differenzengleichungen formuliert werden. Der Bereich ri ≤ r ≤ ra wird in nA Abschnitte der Breite h = (ra− ri)/nA unterteilt. Die Abschnittsgrenzen (nA+1 Punkte) sind die "Stützstellen" für die Differenzengleichung, die die Differenzialgleichung ersetzt. Für einen beliebigen Punkt i gilt:
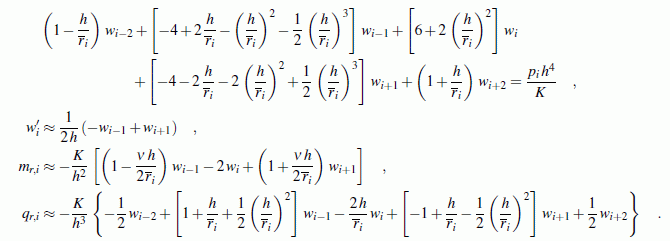
Beispiel
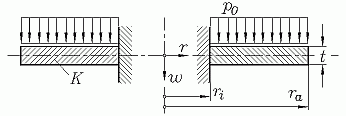
Die skizzierte rotationssymmetrisch belastet und gelagerte Kreisringplatte ist am Innenrand starr eingespannt und am Außenrand frei. Sie trägt die konstante Flächenlast p0. Zu berechnen sind die Durchbiegung w(r) und die Schnittgrößenverläufe mr(r) und qr(r).
Gegeben: ri = 1000 mm ; ra = 3000 mm ; t = 30 mm ; p0 = 0,004 N/mm2 ; E = 2,1·105 N/mm2 ; ν = 0,3 .
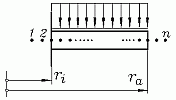
Der Bereich ri ≤ r ≤ ra wird in nA Abschnitte der Breite h = (ra−ri)/nA unterteilt. Es entstehen nA+1 "Innenpunkte". Außerdem werden beim Aufschreiben der Differenzengleichung für alle diese Punkte noch 4 "Außenpunkte" benötigt. Die insgesamt n = nA+5 Punkte werden wie nebenstehend skizziert von 1 bis n nummeriert.
Für die Punkte 3 bis n−2 werden die Differenzengleichungen aufgeschrieben (ri ist der Radius bis zum jeweiligen Punkt i):
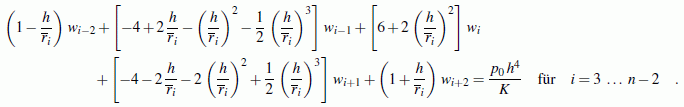
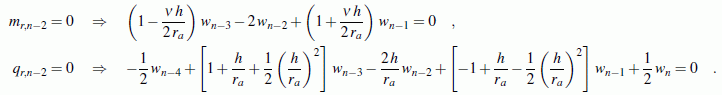
clear all
ri = 1000 ;
ra = 3000 ;
t = 30 ;
E = 2.1e5 ;
ny = 0.3 ;
p0 = 0.004 ;
K = E*t^3/(12*(1-ny^2)) ;
nA = 1000 ; % Anzahl der Abschnitte
n = nA + 5 ; % Anzahl der Gleichungen
h = (ra-ri)/nA ; % Schrittweite
A = zeros (n,7) ; % Rechteckmatrix fuer Aufnahme der Bandmatrix
b = zeros (n,1) ; % Nullvektor ("rechte Seite")
pi = zeros (n,1) ; % Flaechenlastintensitaeten an Stuetzpunkten
r = zeros (n,1) ; % Radien bis zu Stuetzpunkte
iLinks = 3 ; % Nummern der Randpunkte
iRechts = n - 2 ;
pi(1:n) = p0 ; % Belastung
r(iLinks:iRechts) = ri:h:ra ; % Radien
%Randbedingungen:
A(1:2,:) = [0 0 0 0 0 1 0 ;
0 0 0 -1 0 1 0 ] ; % Starr eingespannter Rand links und freier Rand rechts
A(n-1:n,:) = [ -0.5 1+h/ra+h^2/(2*ra^2) -2*h/ra -1+h/ra-h^2/(2*ra^2) 0.5 0 0 ;
1-ny*h/(2*ra) -2 1+ny*h/(2*ra) 0 0 0 0 ] ;
for i = 3:n-2 % Matrix A:
hdr = h/r(i) ;
A(i,:)= [0 1-hdr -4+2*hdr-hdr^2-0.5*hdr^3 6+2*hdr^2 -4-2*hdr-hdr^2+0.5*hdr^3 1+hdr 0] ;
b(i) = pi(i)*h^4/K ; % Standardgleichungen
end
w = gabamp (A , b) ; % Berechnung der Durchsenkung
clf; % Graphische Ausgabe der Biegelinie:
subplot (3,1,1) ; plot (r(3:n-2) , w(3:n-2)) , axis ij , grid on , title ('w(r)') , xlim([0 ra])
for i=3:n-2
hdr = h/r(i) ;
mr(i) = -K*((1-0.5*ny*hdr)*w(i-1) - 2*w(i) + (1+0.5*ny*hdr)*w(i+1))/h^2 ; % Biegemoment
qr(i) = -K*(-0.5*w(i-2) + (1+hdr+0.5*hdr^2)*w(i-1) - 2*hdr*w(i) + ...
(-1+hdr-0.5*hdr^2)*w(i+1) + 0.5*w(i+2))/h^3 ; % Querkraft
end
subplot (3,1,2) ; plot (r(3:n-2) , mr(3:n-2)) , grid on , title ('m_r(r)') , xlim([0 ra])
subplot (3,1,3) ; plot (r(3:n-2) , qr(3:n-2)) , grid on , title ('q_r(r)') , xlim([0 ra])
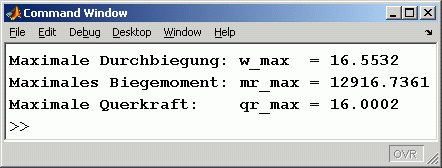
disp(['Maximale Durchbiegung: w_max = ', num2str(max(w))]) ;
disp(['Maximales Biegemoment: mr_max = ', num2str(max(abs(mr)))]) ;
disp(['Maximale Querkraft: qr_max = ', num2str(max(abs(qr)))]) ;
Die Koeffizientenmatrix des Gleichungssystems wird im Matlab-Script
als
"Unsymmetrische Bandmatrix"
Unsymmetrische
Bandmatrizen für Differenzenverfahren (Klicken)
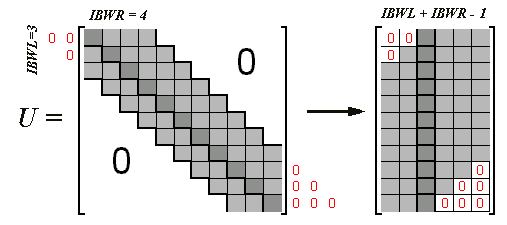kompakt gespeichert. Für die Lösung linearer Gleichungssysteme
mit dieser Speichervariante steht das Script
gabamp.m zur Verfügung.
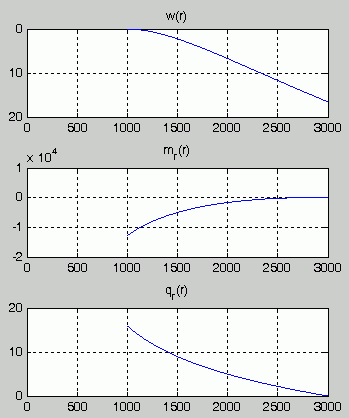
Nebenstehend sieht man die Verläufe der Funktionen w(r), mr(r) und qr(r), die vom Matlab-Script gezeichnet wurden. In das Command Window wurden die jeweiligen Maximalwerte geschrieben:
Verifizieren der Ergebnisse
Weil der Integrationsbereich in nA = 1000 Abschnitte (und damit sehr fein) unterteilt wurde, sind sehr gute Näherungen zu erwarten. Mit folgenden Überlegungen können die Ergebnisse bestätigt werden:
- Qualitativ: Die graphischen Darstellungen entsprechen den Erwartungen. Die Verformung zeigt die Nullverschiebung und die horizontale Tangente an der Einspannstelle, Biegemomentenverlauf und Querkraftverlauf enden beim Wert Null am freien Rand. Aber es sind auch quantitative Kontrollen möglich:
- Die Last p0 wirkt auf einer
Kreisringfläche, so dass ihre Resultierende berechnet werden kann.
Diese Kraft muss mit der Querkraft an der Einspannung,
die auf einem Kreis mit dem Radius
ri wirkt, im Gleichgewicht sein:
Das Gleichgewicht in vertikaler Richtung ist erfüllt.
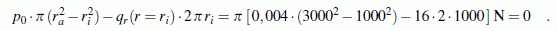
- Die Absenkung am Außenrand kann mit der Absenkung am Rand
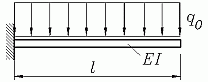
des eingespannten Biegeträgers mit konstanter Linienlast
verglichen werden (nebenstehende Skizze). Man kann sich den
Träger als schmalen Streifen vorstellen, der aus der
Platte herausgeschnitten wurde, z. B. mit der Breite
b = 1 mm und der Länge
l = ra −ri = 2000 mm. Dann hat die
konstante Linienlast die Intensität
q0 = p0·1 mm = 0,004 N/mm.
Der Querschnitt des Trägers ist ein Rechteck mit der Breite
b = 1 mm und der Höhe
t = 30 mm, das für die
Verformungsberechnung benötigte Flächenträgheitsmoment
berechnet sich nach
I = bt3/12 (siehe
Kapitel "Biegung"). Die Formel für die Absenkung des Trägerendes
findet man z. B. im Kapitel "Verformungen durch Biegemomente",
und man berechnet:
Das Ergebnis liegt sehr nah bei dem Wert, der für die Kreisringplatte ermittelt wurde, und auch die Tendenz stimmt: Weil sich bei der Kreisringplatte die Querdehnung nicht (wie beim Biegeträger) frei ausbilden kann, ist die Platte steifer als der Biegeträger (das ist auch der Grund dafür, dass es bei der Kreisringplatte noch ein zweites Biegemoment gibt, worauf auf der Seite "Rotationssymmetrische Kreis- und Kreisringplatten" hingewiesen wird).
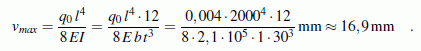
- Die beste Bestätigung findet man allerdings durch eine Rechnung mit einem anderen Verfahren. Dieses Beispiel kann (die Differenzialgleichung der rotationssymmetrischen Kreisplatte ist eine Eulersche Differenzialgleichung) auch noch (mit einiger Mühe) analytisch gelöst werden. Man findet diese Lösung, die im Rahmen der Theorie exakte Ergebnisse liefert, auf der Seite "Rotationssymmetrische Kreisringplatte, Beispiel". Der hier mit dem Differenzenverfahren ermittelte Maximalwert für w(r) weicht vom exakten Wert um weniger als 0,23% ab, die Abweichungen der Maximalwerte für mr(r) und qr(r) sind noch deutlich kleiner.
Download
Das oben gelistete Matlab-Script steht als KreisringplatteDiffVerf.m zum Download zur Verfügung, ebenso das aus diesem Script aufgerufene Script gabamp.m.
