"Flächenmodelle" zeichnen
Das wesentliche Problem beim Zeichnen eines "3D-Flächenmodells", das mit zwei Arrays definiert wird, wie es auf der Seite "Einfache 3D-Modelle" beschrieben wird, besteht darin, dass sich die Flächen gegenseitig (komplett oder teilweise) überdecken. Dies wird wie folgt gelöst und im Beispiel-Programm "Polyarea 1" realisiert:
- Für alle zu zeichnenden Polygone wird der Abstand vom Betrachter berechnet, für die Darstellung in Parallelprojektion kann dies nur ein "symbolischer Abstand" sein.
- Die Polygone werden nach absteigendem Abstand vom Betrachter sortiert.
- Beim Zeichnen in der sortierten Reihenfolge entstehen die am weitesten entfernten Polygone zuerst, und die näher am Betrachter angeordneten Polygone überdecken die dahinter liegenden.
Nebenstehend sieht man eine Zeichenfläche, die einen kleinen Teil des oben genannten Beispiel-Programms realisiert, dafür aber zusätzlich die beschriebene Strategie verdeutlicht. Man kann sich nach Klicken auf "Verzögerung einschalten" vorführen lassen, wie dieses "Step-by-step"-Zeichnen des Objekts das Bild aufbaut.
Nachfolgend wird der Algorithmus beschrieben, der im Beispiel-Programm "Polyarea 1" realisiert ist:
- Im Body-Teil der HTML-Datei wird der Canvas-Bereich mit der id="canvas"
erzeugt, die Zeichenaktion wird gestartet durch eine Anweisung im Body-Tag:
<body onLoad="init();">
- In der JavaScript-Funktion init wird das cavasGI-Objekt erzeugt und einer global vereinbarten Variablen gi zugewiesen, damit es in allen anderen Funktionen verfügbar ist.
- Das aktuelle Modell wird durch zwei global vereinbarte Arrays xyz und area repräsentiert. Beim Start der Seite soll der Würfel sichtbar sein, deshalb werden diesen beiden Arrays die Arrays cubexyz und cubearea (befinden sich in der eingebundenen Datei flaechenmodelle.js) zugewiesen.
- Die 3D-Koordinaten ("World coordinates") der Modelle werden vor der Zeichenaktion unter Berücksichtigung der eingestellten Transformation mit der gültigen Projektion auf ebene "User coordinates" umgerechnet. Um mit der Definition der "User coordinates" für die Zeichenfläche einen "passenden Bereich" vorzusehen, gibt es die Hilfs-Funktion ptlimits, der ein 3D-Koordinaten-Array übergeben wird. Die Funktion liefert die Extremwerte der 2D-Koordinaten ab, die bei der Projektion entstehen. Dies wird hier genutzt, um mit setusercoordsi einen passenden Bereich (bei einem Rand von 20%) einzustellen (die beiden hellblauen Zeilen im folgenden Listing).
- Schließlich wird die Funktion draw aufgerufen, die das Modell zeichnet. So sieht die komplette Funktion init aus:
function init () {
gi = new canvasGI ("canvas") ; // Ein "CanvasGI-Objekt" wird erzeugt
gi.setcurrentviewport (0 , 0 , gi.getcanvaswidth() , gi.getcanvasheight () , gi.XYBOTTOMLEFT) ;
xyz = cubexyz ; // Beim Start soll der Wuerfel ...
area = cubearea ; // erscheinen
var limits = gi.ptlimits (xyz) ; // ermittelt Grenzen der "User coordinates"
gi.setusercoordsi (limits.xumin , limits.yumin , limits.xumax , limits.yumax , 20) ;
fillinput () ; // ... fuellt die Eingabefelder
draw () ; // ... zeichnet das Modell
}
- Die grüne Zeile definiert den gesamten Canvas als "Current viewport", was nicht erforderlich wäre, weil es die Standard-Einstellung ist, legt aber außerdem das Viewport-Koordinatensystem in die linke untere Ecke, was die dort vorgesehene Textausschrift leichter positionieren lässt.
- Mit der Funktion fillinput werden die Eingabefelder, die die Projektionen definieren, vorbelegt.
Die nachfolgend gelistete Funktion draw wird weiter unten erklärt:
function draw () {
var points = new Array () ; // ... fuer die Koordinaten eines Polygons
gi.clearcanvas ("silver" , "black") ; // ... fuellt Canvas-Bereich mit Hintergrundfarbe
// ("silver") und zeichnet schwarzen Rahmen
for (var i = 0 ; i < area.length ; i++) {
var np = area[i].length - 1 ; // ... weil letztes Element die Farbe ist
for (var j = 0 ; j < np ; j++) {
points[j] = xyz[area[i][j]] ; // ... sammelt Punktkoordinaten eines Polygons
}
area[i].unshift (gi.wtsymbdist (points , np)) ; // ... berechnet symbolischen Abstand vom Betrachter
} // und fuegt diesen Wert an der Array-Spitze an
gi.sortbyindex (area , 0) ; // ... sortiert nach den Werten an der Array-Spitze
for (var i = 0 ; i < area.length ; i++) {
area[i].shift() ; // ... entfernt den Wert an der Array-Spitze wieder
var np = area[i].length - 1 ;
for (var j = 0 ; j < np ; j++) {
points[j] = xyz[area[i][j]] ; // ... sammelt Punktkoordinaten eines Polygons
}
gi.wtdrawfarea (points , np , area[i][np] , "black") ;
}
var txt = (gi.getprojectiontype() == gi.PROJ_PARALLEL) ? "Parallelprojektion" : "Zentralprojektion" ;
gi.vdrawtext (txt , 10 , 10 , "black" , "16pt sans-serif") ;
}
- Die Funktion draw besteht im Wesentlichen aus drei Bereichen:
- Im (hellblau dargestellten) Teil werden in einer Schleife über alle Flächen des zu zeichnenden Objekts (für den Würfel also 6) die "symbolischen Abstände" berechnet (mit der CanvasGI-Funktion wtsymbdist) und den Flächeninformationen hinzugefügt. Dafür werden aus den im Array area enthaltenen Punktnummern die Koordinatentripel aus dem Array xyz entnommen und in einem Array points zusammengetellt (dieses enthält dann zum Beispiel für den Würfel np = 6 Koordinatentripel).
- In der (weiß dargestellten) Zeile sortiert die CanvasGI-Funktion sortbyindex die Flächen nach den berechneten Abständen.
- Im (grün dargestellten) Teil werden in einer weiteren Schleife alle Flächen mit der CanvasGI-Funktion wtdrawfarea gezeichnet.
- Die Funktion wtsymbdist
erwartet ein Array points mit np Koordinatentripeln,
aus denen der "Mittelpunkt" des Polygons berechnet wird (arithmetisches
Mittel der einzelnen Koordinaten),
und liefert für diesen Punkt einen "symbolischen Abstand" vom Betrachter ab:
- Bei eingestellter Zentralprojektion wird das Quadrat des Abstandes des Punktes vom "Eye point" abgeliefert.
- Bei eingestellter Parallelprojektion ist der Begriff "Abstand vom Betrachter" ohnehin nicht sinnvoll, weil dieser sich "im Unendlichen" befindet. Deshalb wird ein vorzeichenbehafteter Wert geliefert, der der mit einem konstanten Faktor multiplizierte Abstand des Punktes von der Projektionsebene ist.
- Die Funktion sortbyindex
erwartet ein (mehrdimensionales) Array area und sortiert es
nach den Werten, deren Index als zweiter Parameter übergeben wird.
Beispiel: Für den Würfel werden die 6 Flächen mit dem Array cubearea beschrieben:var cubearea = [ [0 , 1 , 2 , 3 , "magenta" ] , [0 , 3 , 7 , 4 , "cyan" ] , ... , [4 , 5 , 6 , 7 , "red" ] ] ;Mit wtsymbdist wurden aus den zu den Punktnummern gehörenden Koordinaten die "symbolischen Abstände" berechnet und den einzelnen Flächenbeschreibungen (mit unshift) vorangestellt:var cubearea = [ [dist0 , 0 , 1 , 2 , 3 , "magenta" ] , [dist1 , 0 , 3 , 7 , 4 , "cyan" ] , ... , [dist5 , 4 , 5 , 6 , 7 , "red" ] ] ;Nach den auf der Postion 0 stehenden dist-Werten sortiert sortbyindex das Feld. In der nachfolgenden Schleife werden die dist-Werte (mit shift) wieder entfernt. - Die zweite Schleife über alle (nunmehr sortierten) Flächen entspricht im Wesentlichen der ersten Schleife: Aus den im Array area enthaltenen Punktnummern werden die Koordinatentripel aus dem Array xyz entnommen und in einem Array points zusammengetellt, das neben der Anzahl der Punkte np hier allerdings der CanvasGi-Funktion wtdrawfarea übergeben wird, die eine "gefüllte Fläche" zeichnet und dafür als Parameter 3 und 4 noch die Farbinformationen für Füllung bzw. Rand erwartet.
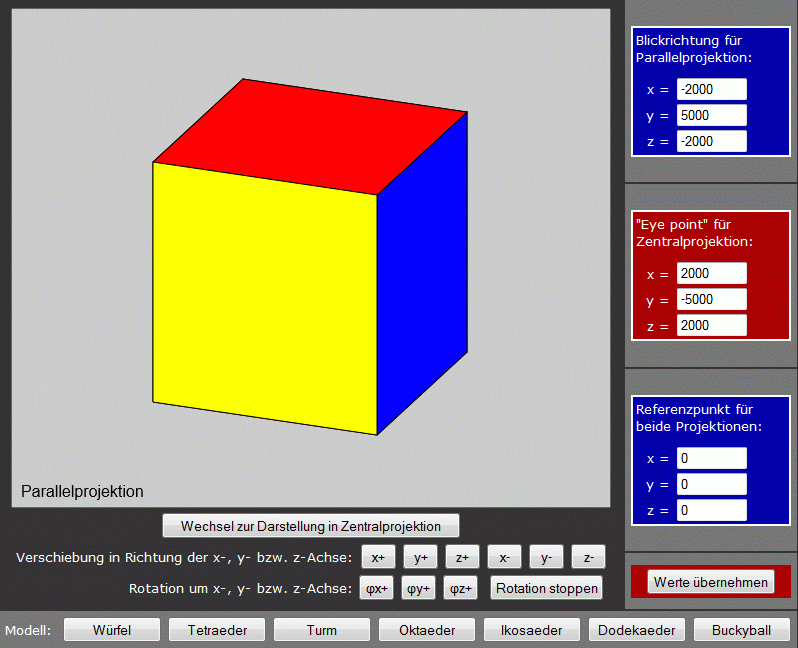
Beipiel-Programm "Polyarea"
Das Beipiel-Programm "Polyarea" enthält neben den oben beschriebenen Funktionen noch wesentlich mehr Angebote. Es startet mit folgendem Bild:
- Der Wechsel zu unterschiedlichen Projektionstypen und die Eingabe von "Blickrichtung", "Eye point" und "Referenzpunkt" sind so realisiert, wie es auf der Seite "Projektionen, Beispiel-Programm Projektion 1" beschrieben ist.
- Die Bewegung des Modells und die Rotation des Modells als Animation entspricht exakt der Realisierung, wie sie auf der Seite "3D-Dahtmodelle zeichnen und animieren" beschrieben wird.
Weiterlesen
- Empfehlung zum Weiterlesen: Auf der Seite "Mehrere 3D-Flächenmodelle zeichnen und animieren" wird gezeigt, wie die hier beschriebene Strategie für das Zeichnen von Flächenmodellen auf mehrere Modelle angewendet und Bewegung in das Bild gebracht werden kann.
- Auf der Seite "3D-Flächen mit unterschiedlicher Lightness zeichnen" werden die hier vorgestellten Modelle einfarbig ohne Zeichnen der Kanten dargestellt, indem unterschiedliche Helligkeit der einzelnen Flächen die Kanten erkennen lässt. Auch für diese Modelle werden Bewegungen realisiert.