Die Strategie der Newton-Cotes-Formeln
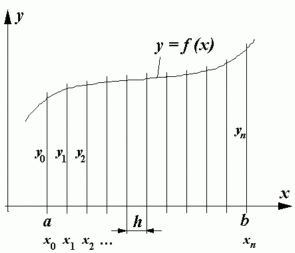
Das Integrationsintervall a ≤ x ≤ b wird in n äquidistante Abschnitte der Breite
unterteilt, es entstehen n+1 "Stützstellen" x0, x1, x2, ... , xn, für die die Funktionswerte y0, y1, y2, ... , yn berechnet werden können.
Durch die so entstandenen Punkte werden bereichsweise Polynomfunktionen gelegt, die auf einfache Weise integriert werden können: Durch je zwei benachbarte Punkte kann jeweils eindeutig eine Grade gelegt werden, durch drei Punkte eine quadratische Parabel usw.
Nach Ausführung der Integration entstehen für die Anwendung sehr handliche Formeln, die umso genauer sind, je höher der Grad der verwendeten Polynomfunktion ist. Bei größer werdendem n konvergieren die Ergebnisse aller Formeln gegen den exakten Wert des Integrals.
Trapezregel
Wenn durch jeweils zwei benachbarte Punkte (xi ,yi) und und (xi+1,yi+1) eine Gerade gelegt wird, ist der schmale Flächenabschnitt zwischen diesen Punkten ein Trapez mit der Höhe h, dessen Fläche sich nach der Formel Ai = (yi + yi+1)·h/2 berechnen lässt. Die Summe aller Teilflächen lässt sich zu folgender Formel zusammenfassen. Es ist die ZUSAMMENGESETZTE TRAPEZREGEL:
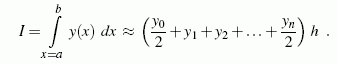
Es lässt sich zeigen, dass mit der Trapezregel ein Fehler (Abweichung vom exakten Wert des bestimmten Integrals) entsprechend
entsteht. Darin ist x eine Stelle innerhalb des Integrationsintervalls a ≤ x ≤ b. Weil diese Stelle nicht bekannt ist, kann der Fehler nicht berechnet werden, aber es sind qualitative Aussagen möglich: Bei feiner werdender Unterteilung des Intervalls nimmt der Fehler quadratisch (proportional h2 → Verfahren 2. Ordnung) ab. Der Fehler verschwindet erwartungsgemäß, wenn die zweite Ableitung des Integranden Null ist (eine Gerade kann natürlich von der Trapezregel exakt erfasst werden).
Simpsonsche Regel
Durch jeweils drei benachbarte Punkte kann eindeutig eine quadratische Parabel gelegt werden. Dann entsteht jeweils eine sich über die Breite 2h erstreckende Teilfläche, die oben durch die Parabel und außerdem durch drei Geraden begrenzt wird. Diese Fläche kann mittels Integration exakt berechnet werden. Die Summe aller Teilflächen lässt sich zu folgender Formel zusammenfassen. Es ist die zusammengesetzte SIMPSONsche Regel:
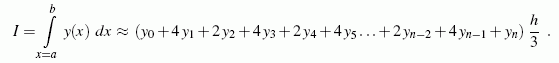
Es ist einleuchtend, dass für die Anwendung dieser Formel n geradzahlig sein muss.
Es lässt sich zeigen, dass mit der Simppsonschen Regel ein Fehler (Abweichung vom exakten Wert des bestimmten Integrals) entsprechend
entsteht. Darin ist x wieder eine Stelle innerhalb des Integrationsintervalls a ≤ x ≤ b. Interessant ist, dass bei feiner werdender Unterteilung des Intervalls der Fehler proportional mit h4 abnimmt (Verfahren 4. Ordnung). Der Fehler verschwindet sogar schon, wenn die vierte Ableitung des Integranden Null ist: Mit der Simpsonschen Regel, die den Integranden stückweise durch eine quadratische Parabel approximiert, können Funktionen 3. Grades exakt integriert werden.
Formeln höherer Ordnung
Man kann dieses Spiel beliebig weiter treiben (und es ist natürlich auch sehr weit getrieben worden): Durch vier Punkte kann eindeutig eine Funktion 3. Grades gelegt werden, mit der eine sich über die Breite 3h erstreckende Teilfläche mittels Integration exakt berechnet werden kann, und die Teilflächen lassen sich zu einer neuen Formel summieren usw.
Das allerdings ist nicht sehr sinnvoll, und die Formeln höherer Ordnung (höher als die Simpsonsche Regel) haben keine praktische Bedeutung. Es ist vielmehr sinnvoll, die oben angegebenen Formeln in eine Strategie einzubetten, die zum Beispiel die Genauigkeitsanforderungen an das Ergebnis iterativ erreichen. Dies wird mit dem Verfahren von Romberg erreicht.

